Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

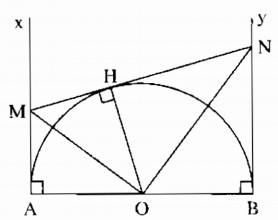
a) Gọi I là tiếp điểm của tiếp tuyến MN với đường tròn (O). Nối OI.
Ta có: ˆAOI+ˆBOI=180∘AOI^+BOI^=180∘ (hai góc kề bù)
OM là tia phân giác cảu góc AOI (tính chất hai tiếp tuyến cắt nhau)
Quảng cáo
ON là tia phân giác của góc BOI (tính chất hai tiếp tuyến cắt nhau)
Suy ra: OM ⊥ ON (tính chất hai góc kề bù)
Vậy ˆMON=90∘MON^=90∘
b) Ta có: MA = MI (tính chất hai tiếp tuyến cắt nhau)
NB = NI (tính chất hai tiếp tuyến cắt nhau)
Mà: MN = MI + IN
Suy ra: MN = AM + BN
c) Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến) theo hệ thức lượng trong tam giác vuông, ta có:
OI2=MI.NIOI2=MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra: AM.BN=OI2=R2AM.BN=OI2=R2.
good luck!

1: Xét (O) có
CA là tiếp tuyến có A là tiếp điểm
CM là tiếp tuyến có M là tiếp điểm
Do đó: OC là tia phân giác của \(\widehat{MOA}\)
Xét (O) có
DB là tiếp tuyến có B là tiếp điểm
DM là tiếp tuyến có M là tiếp điểm
Do đó: OD là tia phân giác của \(\widehat{MOB}\)
Ta có: \(\widehat{COD}=\widehat{COM}+\widehat{DOM}\)
\(=\left(\widehat{MOA}+\widehat{MOB}\right)\cdot\dfrac{1}{2}\)
\(=180^0\cdot\dfrac{1}{2}=90^0\)
hay ΔCOD vuông tại O
Xét (O) có
CA là tiếp tuyến có A là tiếp điểm
CM là tiếp tuyến có M là tiếp điểm
Do đó: CM=CA
Xét (O) có
DB là tiếp tuyến có B là tiếp điểm
DM là tiếp tuyến có M là tiếp điểm
Do đó: DB=DM
\(AC\cdot BD=CM\cdot MD=OM^2\) không phụ thuộc vào vị trí của M

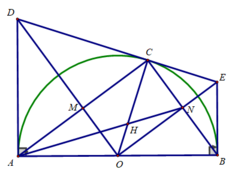
b) Xét tứ giác OMCN có:
∠(OMC) = 90 0 (AC ⊥ OD)
∠(ONC) = 90 0 (CB ⊥ OE)
∠(NCM) = 90 0 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật

Gọi H là chân đường vuông góc hạ từ O xuống CD
Ta CM : OH = OB = R ( O )
Tia CO cắt tia đối của tia By tại E
Xét tam giác OAC và OBE có :
góc A + góc B = 900 ( t/c tiếp tuyến )
góc AOC = BOE ( đối đỉnh )
OA = OB (=R)
=> tam giác OAC = OBE ( g.c.g ) => OC = OE
Tam giác DEC có DO vừa là đường cao vừa là trung tuyến nên là tam giác cân. Khi đó DO cũng là đường phân giác
=> Ta có : OH vuông góc CD, OH = OB = R ( O ) nên CD tiếp xúc với (O) tại H


khong biet lam
Bạn học lớp mấy mà bạn không biết trả lời câu hỏi dễ như vậy?