Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) Theo bài ra ta có
\(\widehat{ANB}=\widehat{BMA}=90^o\)( Góc nội tiếp chắn nửa đg tròn) \(\Rightarrow\widehat{KNA}=\widehat{KMB}=90^o\)
\(\Rightarrow\widehat{KNA}+\widehat{KMB}=90^o+90^o=180^o\)
\(\Rightarrow\) Tứ giác KMIN nội tiếp đường tròn đường kính KI

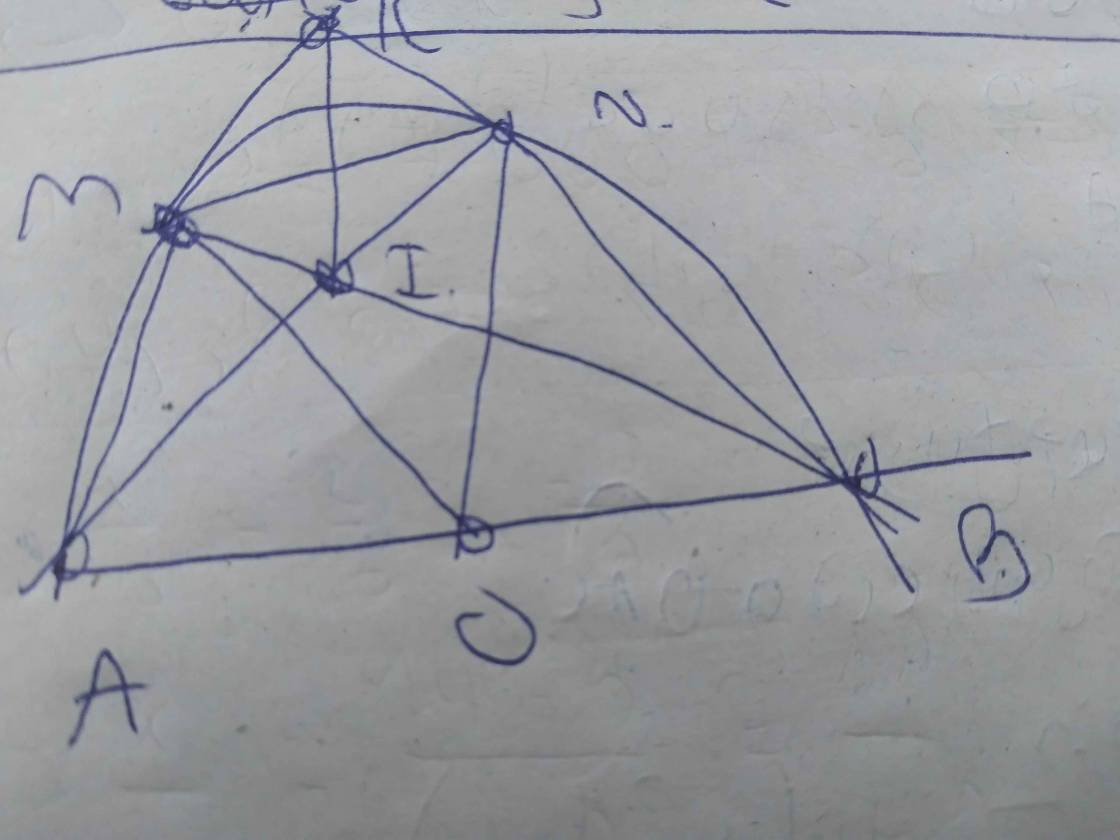
a: góc AMB=góc APB=1/2*sđ cung AB=90 độ
góc QMN+góc QPN=180 độ
=>QMNP là tứ giác nội tiếp
b: Xét ΔQBA có
AP,BM là đường cao
AP cắt BM tại N
=>N là trực tâm
=>QN vuông góc AB tại E
Xét ΔMAB vuông tại A và ΔMNQ vuông tại M có
góc MAB=góc MNQ(=góc ENB)
=>ΔMAB đồng dạng với ΔMNQ
c: Gọi F là trung điểm của QN
=>F là tâm đường tròn ngoại tiếp ΔMNQ
góc FMO=góc FMN+góc OMN
=góc FNM+góc OBN
=góc OBN+góc ENB=90 độ
=>MO là tiếp tuyến của đường tròn ngoại tiếp ΔMNQ


a, ANM =90 độ góc nt chắn nửa dt => ANK= 90 ( kề bù )
AMB= 90 ( góc nt..) => Xét tg KMIN có : ANK =AMB mà AMB là góc ngoài tại đỉnh M => tg KMIN nt
b. Xét tg KMN và tg KBA : K chung
ABK=KMN ( tg AMNB nt )
=> 2 tg ấy đồng dạng => KM/KN=KB/KA => km.ka=kn.kb