Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Theo tính chất 2 tiếp tuyến cắt nhau (MAMA, MCMC) thì MA=MCMA=MC
Mà OA=OC=ROA=OC=R
⇒MO⇒MO là đường trung trực của ACAC
⇒MO⊥AC⇒MEAˆ=900(1)⇒MO⊥AC⇒MEA^=900(1)
Lại có:
ADBˆ=900ADB^=900 (góc nt chắn nửa đường tròn)
⇒MDAˆ=1800−ADBˆ=900(2)⇒MDA^=1800−ADB^=900(2)
Từ (1);(2) ⇒MEAˆ=MDAˆ⇒MEA^=MDA^. Mà 2 góc này cùng nhìn cạnh MAMA nên tứ giác AMDEAMDE là tgnt.
cảm ơn bn
nhưng mik còn câu c thôi
mà bn chép mạng cx chọn cái chép đi chứ, chép thừa r

.png)
a) Vì MA, MC là tiếp tuyến nên: ˆMAO=ˆMCO=900⇒MAO^=MCO^=900⇒ AMCO là tứ giác nội tiếp đường tròn đường kính MO.
ˆADB=900ADB^=900 góc nội tiếp chắn nửa đường tròn) ⇒ˆADM=900⇒ADM^=900 (1)
Lại có: OA = OC = R; MA = MC (tính chất tiếp tuyến). Suy ra OM là đường trung trực của AC
⇒ˆAEM=900⇒AEM^=900 (2).
Từ (1) và (2) suy ra MADE là tứ giác nội tiếp đường tròn đường kính MA.
b) Tứ giác AMDE nội tiếp suy ra: ˆADE=ˆAME=ˆAMOADE^=AME^=AMO^ (góc nội tiếp cùng chắn cung AE) (3)
Tứ giác AMCO nội tiếp suy ra: ˆAMO=ˆACOAMO^=ACO^(góc nội tiếp cùng chắn cung AO) (4).
Từ (3) và (4) suy ra ˆADE=ˆACOADE^=ACO^
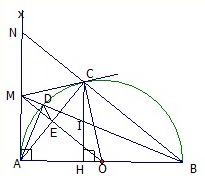
c) Tia BC cắt Ax tại N. Ta có ˆACB=900ACB^=900 (góc nội tiếp chắn nửa đường tròn) ⇒ˆACN=900⇒ACN^=900, suy ra ∆ACN vuông tại C. Lại có MC = MA nên suy ra được MC = MN, do đó MA = MN (5).
Mặt khác ta có CH // NA (cùng vuông góc với AB) nên theo định lí Ta-lét thì ICMN=IHMA(=BIBM)ICMN=IHMA(=BIBM) (6).
Từ (5) và (6) suy ra IC = IH hay MB đi qua trung điểm của CH.
Để giải quyết bài toán này, ta sử dụng định lí Menelaus và định lí Stewart.
Bước 1: Chứng minh AD/AC + AM/AN = 3.
Áp dụng định lí Menelaus cho tam giác AGC với đường thẳng cắt AC, ID, MG, ta có:
$\dfrac{IM}{MD} \cdot \dfrac{DN}{NC} \cdot \dfrac{CG}{GA} = 1$
Do $CG = 2 \cdot GA$ và $DN = AN - AD = AN - 2\cdot AI$, ta có thể đưa về dạng:
$\dfrac{IM}{MD} \cdot \dfrac{AN-2\cdot AI}{NC} = \dfrac{1}{2}$
Từ định lí Stewart, ta có $4\cdot AI\cdot DI + AD^2 = 3\cdot ID^2$, do đó $ID = \dfrac{AD}{\sqrt{3}}$.
Thay vào phương trình trên, ta được:
$\dfrac{IM}{MD} \cdot \dfrac{AN-AD}{NC} = \dfrac{1}{\sqrt{3}}$
Tương đương với:
$\dfrac{IM}{MD} \cdot \dfrac{AD}{NC} + \dfrac{IM}{MD} \cdot \dfrac{AM}{AN} = \dfrac{1}{\sqrt{3}} + \dfrac{AD}{NC}$
Từ đó suy ra:
$\dfrac{AM}{AN} + \dfrac{AD}{AC} = \dfrac{3}{\sqrt{3}}$
Do đó:
$\dfrac{AD}{AC} + \dfrac{AM}{AN} = 3$ (Đpcm)

O A B x C E D M
a, xét tg AEO và CEO có : EO chung
^AEO = ^CEO = 90
OA = OC = r
=> Tg AEO = tg CEO (ch-cgv)
=> ^AOE = ^COE
xét tg MAO và tg MCO có : Mo chung
OA = OC = r
=> tg MAO = tg MCO (cg-c)
=> ^MAO = ^MCO
mà ^MAO = 90
=> ^MCO = 90 => OC _|_ MC
có C thuộc 1/2(o)
=> MC là tt của 1/2(o)
b, xét tứ giác MCOA có : ^MCO = ^MAO = 90
=> ^MCO + ^MAO = 180
=>MCOA nội tiếp
+ có D thuộc 1/(o) dk AB (gt) => ^ADB = 90 = ADM
có MEA = 90 do AC _|_ MO (Gt)
=> ^ADM = ^MEA = 90
=> MDEA nt

a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)MB tại D
Xét (O) có
MA,MC là các tiếp tuyến
Do đó: MA=MC
=>M nằm trên đường trung trực của AC(1)
Ta có: OA=OC
=>O nằm trên đường trung trực của AC(2)
Từ (1),(2) suy ra MO là đường trung trực của AC
=>MO\(\perp\)AC tại E và E là trung điểm của AC
Xét tứ giác AEDM có \(\widehat{AEM}=\widehat{ADM}=90^0\)
nên AEDM là tứ giác nội tiếp
b: Xét ΔMAB vuông tại A có AD là đường cao
nên \(MD\cdot MB=MA^2\)
c: Gọi F là giao điểm của BC và MA
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)FB tại C
=>ΔACF vuông tại C
Ta có: CH\(\perp\)AB
MA\(\perp\)AB
Do đó: CH//MA
Gọi I là giao điểm của CH và MB
Ta có: \(\widehat{MAC}+\widehat{MFC}=90^0\)(ΔACF vuông tại C)
\(\widehat{MCA}+\widehat{MCF}=\widehat{FCA}=90^0\)
mà \(\widehat{MAC}=\widehat{MCA}\)(ΔMAC cân tại M)
nên \(\widehat{MFC}=\widehat{MCF}\)
=>MF=MC
mà MA=MC
nên MA=MF(3)
Xét ΔBMA có IH//MA
nên \(\dfrac{IH}{MA}=\dfrac{BI}{BM}\left(4\right)\)
Xét ΔBMF có CI//MF
nên \(\dfrac{CI}{MF}=\dfrac{BI}{BM}\left(5\right)\)
Từ (3),(4),(5) suy ra IC=IH
=>I là trung điểm của CH
=>MB đi qua trung điểm của CH