Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a.
Ta thấy $\widehat{ACB}=\widehat{ADB}=90^0$ (góc nội tiếp chắn nửa đường tròn)
$\Rightarrow \widehat{ECF}=180^0-\widehat{ACB}=180^0-90^0=90^0$; $\widehat{EDF}=180^0-\widehat{ADB}=180^0-90^0=90^0$
Tứ giác $ECFD$ có tổng 2 góc đối $\widehat{ECF}+\widehat{EDF}=90^0+90^0=180^0$ nên $ECFD$ là tứ giác nội tiếp.
b.
Vì $ECFD$ là tứ giác nội tiếp nên $\widehat{AEF}=\widehat{CEF}=\widehat{CDF}=\widehat{ADC}$ (góc nt chắn cung $CF$)

Ta có: ˆACD=900ACD^=900 (góc nội tiếp chắn nửa đường tròn đường kính AD)
Xét tứ giác DCEF có:
ˆACD=900ACD^=900 (cm trên)
ˆEFD=900EFD^=900 (vì EF⊥ADEF⊥AD (gt))
⇒ˆACD+ˆEFD=1800⇒ACD^+EFD^=1800
=> Tứ giác DCEF là tứ giác nội tiếp đường tròn (đpcm).
b) Vì tứ giác DCEF là tứ giác nội tiếp (chứng minh câu a)
⇒ˆC1=ˆD1⇒C1^=D1^ (góc nội tiếp cùng chắn cung EF) (1)
Mà ⇒ˆC2=ˆD1⇒C2^=D1^ (góc nội tiếp cùng chắn cung AB) (2)
Từ (1) và (2) ⇒ˆC1=ˆC2⇒C1^=C2^
⇒⇒ CA là tia phân giác của ˆBCFBCF^ (đpcm)
k đúng hộ

VE HINH
â) Xét tứ giác KCID ,co:
gocI = (cungAB+cungCD):2 = (180+60):2 = 120 độ
gocK=(cungAB-cungCD):2 =(180-60):2=60 độ
gócI+gocK=120do+60do=180 do
Vay : tứ giác KCID nội tiếp (tổng số đo 2 góc đối diện=180 độ )
:góc AKB = 60 độ
b)Ta có:AB//CD
=>cungAC=cungBD=(180-60):2=60 do (2 cung nằm giữa 2 dây song song thì = nhau )
=>AC=BD(2 dây chan 2 cung = nhau thi = nhau ) (1)
=>tứ giác ACDB là hình thang cân
***Xét : 3giac AKDva 3giac BKC ,co:
gocD=gocC=90do (vi gocC va gocD là góc nội tiếp chắn nửa đường tròn)
gocCAD=gocDBC(2goc noi tiep cung chan cungCD)
AD=BC(2 đường chéo của hình thang cân thì = nhau )(cmt)
Do do:3giacAKD =3giacBKC (g-c-g)
=>KD=KC (2 canh tương ứng) (2)
Ta lại có :KA=KC+AC(C nam giua A va K)
}(3)
:KB=KD+BD(D nam giua B va K)
Tu (1) ,(2) va (3) suy ra KA=KB (4)
Tu (2) va (4) suy ra KA.KC=KB.KD .

a) Chứng minh tứ giác IEHFIEHF nội tiếp được đường tròn.
Ta có ∠AEB=∠AFB=900∠AEB=∠AFB=900 (góc nội tiếp chắn nửa đường tròn) ;
⇒AE⊥EB,AF⊥EB⇒AE⊥EB,AF⊥EB hay BE⊥AI;AF⊥BI⇒∠IEH=∠IFH=900BE⊥AI;AF⊥BI⇒∠IEH=∠IFH=900.
Xét tứ giác IEHFIEHF có: ∠IEH+∠IFH=900+900=1800⇒∠IEH+∠IFH=900+900=1800⇒ Tứ giác IEHFIEHF là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 18001800).
b) Chứng minh ∠AIH=∠ABE∠AIH=∠ABE.
Cách 1:
Ta có IEHFIEHF là tứ giác nội tiếp (cmt) ⇒∠EIH=∠EFH⇒∠EIH=∠EFH (hai góc nội tiếp cùng chắn cung EHEH)
Hay ∠AIH=∠EFA.∠AIH=∠EFA.
Mà ∠EBA=∠EFA∠EBA=∠EFA (hai góc nội tiếp cùng chắn cung AFAF của (O)(O))
⇒∠AIH=∠ABE(=∠EFH).(dpcm)⇒∠AIH=∠ABE(=∠EFH).(dpcm)
Cách 2:
Xét tam giác IABIAB có hai đường cao AF,BEAF,BE cắt nhau tại H⇒HH⇒H là trực tâm tam giác IABIAB.
⇒IH⊥AB⇒IH⊥AB hay IK⊥ABIK⊥AB tại KK.
Xét tam giác vuông AIKAIK có: ∠AIK+∠IAK=900⇔∠AIH+∠IAB=900∠AIK+∠IAK=900⇔∠AIH+∠IAB=900.
Xét tam giác vuông ABEABE có: ∠ABE+∠EAB=900⇔∠ABE+∠IAB=900∠ABE+∠EAB=900⇔∠ABE+∠IAB=900.
Do đó ∠AIH=∠ABE∠AIH=∠ABE.
c) Chứng minh cos∠ABP=PK+BKPA+PBcos∠ABP=PK+BKPA+PB.
Nối PA,PBPA,PB ta có ∠APB=900∠APB=900 (góc nội tiếp chắn nửa đường tròn).
Xét tam giác BPKBPK và tam giác BAPBAP có:
∠ABP∠ABP chung;
∠BKP=∠BPA=900;∠BKP=∠BPA=900;
⇒ΔBPK∼ΔBAP(g.g)⇒PKPA=BKPB⇒ΔBPK∼ΔBAP(g.g)⇒PKPA=BKPB (hai cặp cạnh tương ứng tỉ lệ).
Áp dụng tính chất dãy tỉ số bằng nhau ta có: PKPA=BKPB=PK+BKPA+PBPKPA=BKPB=PK+BKPA+PB (1).
Xét tam giác vuông BKPBKP ta có: cos∠ABP=cos∠KPB=BKPBcos∠ABP=cos∠KPB=BKPB (2).
Từ (1) và (2) ta có cos∠ABP=PK+BKPA+PBcos∠ABP=PK+BKPA+PB.
d) Gọi SS là giao điểm cuả tia BFBF và tiếp tuyến tại AA của nửa đường tròn (O)(O). Khi tứ giác AHISAHIS nội tiếp được đường tròn, chứng minh EFEF vuông góc với EKEK.
Xét tứ giác AEHKAEHK có: ∠AEH+∠AKH=900+900=1800⇒∠AEH+∠AKH=900+900=1800⇒ Tứ giác AEHKAEHK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 18001800).
⇒∠HEK=∠HAK=FAB⇒∠HEK=∠HAK=FAB (hai góc nội tiếp cùng chắn cung HKHK);
Lại có ∠FAB=∠FEB∠FAB=∠FEB (hai góc nội tiếp cùng chắn cung FBFB của (O)(O));
⇒∠HEK=∠FEB⇒EB⇒∠HEK=∠FEB⇒EB là phân giác của ∠FEK∠FEK ⇒∠FEK=2∠FEB=2∠FAB⇒∠FEK=2∠FEB=2∠FAB (3).
Ta có: {IH⊥AB(cmt);SA⊥AB(gt)⇒IH//SA⇒{IH⊥AB(cmt);SA⊥AB(gt)⇒IH//SA⇒ Tứ giác AHISAHIS là hình thang (Tứ giác có 2 cạnh đối song song).
Khi AHISAHIS là tứ giác nội tiếp thì ∠SAH+∠SIH=1800∠SAH+∠SIH=1800 (tổng hai góc đối của tứ giác nội tiếp) ;
Mà ∠SAH+∠AHI=1800∠SAH+∠AHI=1800 (hai góc trong cùng phía bù nhau) ;
⇒∠SIH=∠AHI⇒⇒∠SIH=∠AHI⇒ Tứ giác AHISAHISlà hình thang cân.
Do đó ∠ISA=∠SAH∠ISA=∠SAH (Tính chất hình thang cân) hay ∠BSA=∠SAF∠BSA=∠SAF.
Mà ∠SAF=∠SBA∠SAF=∠SBA (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AFAF );
⇒∠BSA=∠SBA⇒ΔSAB⇒∠BSA=∠SBA⇒ΔSAB vuông cân tại A⇒∠SBA=450A⇒∠SBA=450.
⇒ΔFAB⇒ΔFAB vuông cân tại F⇒∠FAB=450F⇒∠FAB=450 (4).
Từ (3) và (4) ta có ∠FEK=2∠FAB=2.450=900∠FEK=2∠FAB=2.450=900.
Vậy khi tứ giác AHISAHIS nội tiếp được đường tròn, chứng minh EFEF vuông góc với EKEK(đpcm).
a, ta có : góc AEB = 90 độ
suy ra góc HEI = 90 độ
tương tự ta có góc HFI = 90 độ
suy ra : góc HEI + góc HFI = 180 độ
suy ra IEHF nội tiếp đường tròn
b, góc AIH = AFE
mà góc ABE = góc AFE
suy ra góc AIH = góc ABE
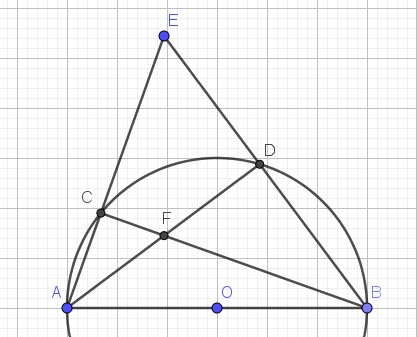
a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
Xét tứ giác ABEF có \(\widehat{ABE}+\widehat{AFE}=90^0+90^0=180^0\)
nên ABEF là tứ giác nội tiếp
b: Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
Xét ΔAFE vuông tại F và ΔACD vuông tại C có
\(\widehat{FAE}\) chung
Do đó: ΔAFE~ΔACD
=>\(\dfrac{AF}{AC}=\dfrac{AE}{AD}\)
=>\(AF\cdot AD=AC\cdot AE\)
c: Gọi M là giao điểm của AB và CD
Xét ΔMAD có
AC,DB là các đường cao
AC cắt DB tại E
Do đó: E là trực tâm của ΔMAD
=>ME\(\perp\)AD
mà EF\(\perp\)AD
và ME,EF có điểm chung là E
nên M,E,F thẳng hàng
Xét tứ giác MBEC có \(\widehat{MBE}+\widehat{MCE}=90^0+90^0=180^0\)
nên MBEC là tứ giác nội tiếp
Xét tứ giác CEFD có \(\widehat{ECD}+\widehat{EFD}=90^0+90^0=180^0\)
nên CEFD là tứ giác nội tiếp
Ta có: \(\widehat{EBF}=\widehat{EAF}\)(ABEF nội tiếp)
\(\widehat{CBE}=\widehat{CME}\)(CMBE nội tiếp)
mà \(\widehat{EAF}=\widehat{CME}\left(=90^0-\widehat{MDA}\right)\)
nên \(\widehat{EBF}=\widehat{EBC}\)
=>BE là phân giác của góc CBF
Ta có: \(\widehat{BFE}=\widehat{BAE}\)(ABEF nội tiếp)
\(\widehat{CFE}=\widehat{CDE}\)(ECDF nội tiếp)
mà \(\widehat{BAE}=\widehat{CDE}\left(=90^0-\widehat{AMC}\right)\)
nên \(\widehat{BFE}=\widehat{CFE}\)
=>FE là phân giác của góc BFC
Xét ΔBCF có
BE,FE là các đường phân giác
BE cắt FE tại E
Do đó: E là tâm đường tròn nội tiếp ΔBCF