
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

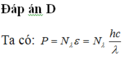
![]()

Nhận thấy: \(2,55=-13,6\cdot\left(\dfrac{1}{4^2}-\dfrac{1}{2^2}\right)\left(eV\right)\)
Suy ra nguyên tử đã nhảy từ mức n=2 lên mức n=4
Tức là, bước sóng nhỏ nhất sinh ra khi nguyên tử nhảy từ mức n=4 về n=1
Khi đó nguyên tử phát ra photon có năng lượng: \(E=-13,6\cdot\left(\dfrac{1}{4^2}-\dfrac{1}{1^2}\right)=12,75\left(eV\right)\)
\(\Rightarrow\lambda=\dfrac{hc}{E}=\dfrac{6,625.10^{-34}\cdot3.10^8}{12,75\cdot1,6.10^{-19}}=9,74.10^{-8}\left(m\right)\)
Chọn A

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

Do E và B biến thiên cùng pha nên, khi cảm ứng từ có độ lớn B0/2 thì điện trường E cũng có độ lớn E0/2.
Bài toán trở thành tính thời gian ngắn nhất để cường độ điện trường có độ lớn E0/2 đang tăng đến độ lớn E0/2.
E M N Eo Eo/2
Từ giản đồ véc tơ quay ta dễ dang tính được thời gian đó là t = T/3
Suy ra: \(t=\dfrac{5}{3}.10^{-7}\)s

Vị trí cực đại giao thoa với hai nguồn cùng pha thỏa mãn điều kiện: \(d_1-d_2=k\lambda\)
Đường cực đại thứ nhất đi qua M1 thỏa mãn: \(d_1-d_2=1.\lambda=16cm\)(1)
Đường cực đại thứ 5 đi qua M2 thỏa mãn: \(d_1'-d_2'=5\lambda=24cm\)(2)
Lấy (2) - (1) vế với vế ta được: \(4\lambda=8\Leftrightarrow\lambda=2cm\)
Vận tốc: \(v=\lambda.f=2.10=20\)(cm/s)
Bạn sử dụng điều kiện cực đại giao thoa của 2 dao động cùng pha.

Khi tạo thành giao thoa, trên đoạn \(S_1S_2\), khoảng cách giữa 2 cực đại liên tiếp là \(\frac{\lambda}{2}\)
Suy ra: \(6\frac{\lambda}{2}=12\Rightarrow\lambda=4mm\)
Tốc độ truyền sóng: \(v=\lambda.f=4.50=200\)(mm/s) = 20 (cm/s)