Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(\frac{x-y}{z-y}=-10\Leftrightarrow x-y=10\left(y-z\right)\)
\(\Leftrightarrow x-y=10y-10z\)
\(\Leftrightarrow x=11y-10z\)
Thay x=11y-10z vào biểu thức \(\frac{x-z}{y-z}\), ta có:
\(\frac{11y-10z-z}{y-z}=\frac{11y-11z}{y-z}=\frac{11\left(y-z\right)}{y-z}=11\)
Chá quá, có ghi nhìn không rõ đề
2) \(2x^2=9x-4\)
\(\Leftrightarrow2x^2-9x+4=0\)
\(\Leftrightarrow2x^2-8x-x+4=0\)
\(\Leftrightarrow2x\left(x-4\right)-1\left(x-4\right)\)
\(\Leftrightarrow\left(2x-1\right)\left(x-4\right)=0\)
\(\Leftrightarrow2x-1=0\) hoặc x-4=0
1) 2x-1=0<=>x=1/2
2)x-4=0<=>x=4(Loại)
=> x=1/2

ta co :
(x+y+z).(x/(z+y)+y/(z+x)+z/(x+y))=1
ban cu phan tich cai bieu thuc tren thi ket qua thu duoc se la:
x^2/(z+y)+y^2/(x+z)+z^2/(x+y)+z+x+y=1
ma x+y+z=1===>dpcm

Bài 2 :
a ) \(25-20x+4x^2=0\)
\(\Leftrightarrow\left(5-2x\right)^2=0\)
\(\Leftrightarrow5-2x=0\Rightarrow x=\dfrac{5}{2}\)
Vậy \(x=\dfrac{5}{2}\)
a,\(\left(-2x^2+3x\right)\left(x^2-x+3\right)\\ \Leftrightarrow-2x^4+2x^3-6x^2+3x^3-3x^2+9x\\ \Leftrightarrow-2x^4+5x^3-3x^2+3x\)
\(b,x\left(x-2\right)\left(x+2\right)-\left(x-3\right)\left(x^2+3x+9+6\right)+6\left(x+1\right)^2=15\\ \Leftrightarrow x\left(x^2-4\right)-\left(x^3-27\right)+6\left(x^2+2x+1\right)=15\\ \Leftrightarrow x^3-4x-x^3+27+6x^2+12x+6=15\\ \Leftrightarrow6x^2+8x+18=0\\ \Leftrightarrow6\left(x^2+\dfrac{4}{3}x+3\right)=0\\ \Leftrightarrow\left(x+\dfrac{2}{3}\right)^2+\dfrac{23}{9}=0\)
Với mọi x thì \(\left(x+\dfrac{2}{3}\right)^2\ge0\Rightarrow\left(x+\dfrac{2}{3}\right)^2+\dfrac{23}{9}>0\)
Do đó ko tìm đc giá trị nào của x thỏa mãn đề bài
Vậy..

Đề số 3.
1.
a,\(4x\left(5x^2-2x+3\right)\)
\(=20x^3-8x^2+12x\)
b.\(\left(x-2\right)\left(x^2-3x+5\right)\)
\(=x^3-3x^2+5x-2x^2+6x-10\)
\(=x^3-5x^2+11x-10\)
c,\(\left(10x^4-5x^3+3x^2\right):5x^2\)
\(=2x^2-x+\dfrac{3}{5}\)
d,\(\left(x^2-12xy+36y^2\right):\left(x-6y\right)\)
\(=\left(x-6y\right)^2:\left(x-6y\right)\)
\(=x-6y\)
2.
a,\(x^2+5x+5xy+25y\)
\(=\left(x^2+5x\right)+\left(5xy+25y\right)\)
\(=x\left(x+5\right)+5y\left(x+5\right)\)
\(=\left(x+5y\right)\left(x+5\right)\)
b,\(x^2-y^2+14x+49\)
\(=\left(x^2+14x+49\right)-y^2\)
\(=\left(x+7\right)^2-y^2\)
\(=\left(x+7-y\right)\left(x+7+y\right)\)
c,\(x^2-24x-25\)
\(=x^2+25x-x-25\)
\(=\left(x^2-x\right)+\left(25x-25\right)\)
\(=x\left(x-1\right)+25\left(x-1\right)\)
\(=\left(x+25\right)\left(x-1\right)\)
3.
a,\(5x\left(x-3\right)-x+3=0\)
\(5x\left(x-3\right)-\left(x-3\right)=0\)
\(\left(5x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=1\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=3\end{matrix}\right.\)
Vậy \(x=\dfrac{1}{5}\) hoặc \(x=3\)
b.\(3x\left(x-5\right)-\left(x-1\right)\left(2+3x\right)=30\)
\(3x^2-15x-\left(2x+3x^2-2-3x\right)=30\)
\(3x^2-15x-2x-3x^2+2+3x=30\)
\(-14x+2=30\)
\(-14x=28\)
\(x=-2\)
c,\(\left(x+2\right)\left(x+3\right)-\left(x-2\right)\left(x+5\right)=0\)
\(x^2+3x+2x+6-\left(x^2+5x-2x-10\right)=0\)
\(x^2+5x+6-x^2-5x+2x+10=0\)
\(2x+16=0\)
\(2x=-16\)
\(x=-8\)
Mình học chật hình không giúp bạn được.Xin lỗi!

Câu 3 ( Đề 1)
a) A = ( x - 2)2 - ( x + 3)( x - 3)
A = x2 - 4x + 4 - x2 + 9
A = - 4x + 13
b) B = 4x( x + 3) - 3x(4 + x)
B = 4x2 + 12x - 12x - 3x2
B = x2
Câu 4 . a) 5x3 - 45x
= 5x( x2 - 32)
= 5x( x - 3)( x + 3)
b) 5x2 + 5xy - x - y
= 5x( x + y) - ( x +y)
= ( x + y)( 5x - 1)
c) x3 - 9x2y + xy2 - 9y3
= x( x2 + y2) - 9y( x2 + y2)
= ( x2 + y2)( x - 9y)
Câu 3 : ( đề 2)
a) A = ( x - 2)2 -( x + 1)( x - 1) - x( 1 - x)
A= x2 - 4x + 4 - x2 + 1 - x + x2
A = x2 - 5x + 5
b)B = 7x( x - 4) - 2x( x - 6)
B = 7x2 - 28x - 2x2 + 12x
B = 5x2 - 16x
Cau 4 .
a) 4x3 - 64x
= 4x( x2 - 42)
= 4x( x - 4)( x + 4)
b) x3 + x + 5x2 + 5
= x( x2 + 1) + 5( x2 + 1)
= ( x2 + 1)( x + 5)
c) x2 - 3xy - 10y2
= x2 - (2y)2 - 3xy - 6y2
= ( x - 2y)( x + 2y) - 3y( x + 2y)
= ( x + 2y)( x - 5y)
Cau 5 . 4x2 - 5x + x3 - 20
= x2( x + 4) - 5( x + 4)
= ( x + 4)( x2 - 5)
Vay phep chia : ( 4x2 - 5x + x3 - 20) cho da thuc ( x + 4) duoc thuong la x2 - 5
bài 4
a) 4x3-64x
= 4x(x2-16)
b)x3+x+5x2+5
= (x3+x)+(5x2+5)
= x(x2+1)+5(x2+1)
= (x2+1)(x+5)


a) x3 - 4x2 + 4x
= x(x2 - 4x + 4)
= x(x - 2)2
b) x2 - 3x + 2
= x2 - x - 2x + 2
= (x2 - x) + (2x - 2)
= x(x - 1) + 2(x - 1)
= (x + 2)(x - 1)
c) 8x3 + \(\dfrac{1}{27}\)
= \(\left(2x+\dfrac{1}{3}\right)\)\(\left(4x^2-\dfrac{2}{3}x+\dfrac{1}{9}\right)\)
d) 64x3 - \(\dfrac{1}{8}\)
= \(\left(4x+\dfrac{1}{2}\right)\left(16x^2-2x+\dfrac{1}{4}\right)\)
e) x2 - 4 + (x - 2)2
= (x + 2)(x - 2) - (x - 2)2
= (x - 2)[(x + 2) - (x - 2)]
= (x - 2)(x + 2 - x + 2)
= 4(x - 2)
f) x3 - 2x3 + x - xy2
= -x3 + x - xy2
= -x(x2 - 1 + y2)
g) x3 - 4x2 - 12x + 27
= (x3 + 27) - (4x2 + 12x)
= (x + 3)(x2 - 3x + 9) - 4x(x + 3)
= (x + 3)[(x2 - 3x + 9) - 4x]
= (x + 3)(x2 - 3x + 9 - 4x)
= (x + 3)(x2 - 7x + 9)
h) 2x - 2y - x2 + 2xy - y2
= (2x - 2y) - (x2 - 2xy + y2)
= 2(x - y) - (x - y)2
= (x - y)(2 - x + y)
i) 3x2 + 6x + 3 - 3y2
= 3(x2 + 2x + 1 - y2)
= 3[(x2 + 2x + 1) - y2]
= 3[(x + 1)2 - y2]
= 3( x + 1 - y)(x + 1 + y)
k) 25 - x2 - y2 + 2xy
= 25 - (x2 - 2xy + y2)
= 25 - (x - y)2
= (5 - x + y)(5 + x - y)
l) 3x - 3y - x2 + 2xy - y2
= (3x - 3y) - (x2 - 2xy + y2)
= 3(x - y) - (x - y)2
= (x - y)(3 - x + y)
m) x2 - y2 + 2x - 2y
= (x2 - y2) + (2x - 2y)
= (x - y)(x + y) + 2(x - y)
= (x - y)(x + y + 2)
n) x4 + 2x3 - 4x - 4
= (x4 - 4) + (2x3 - 4x)
= (x2 - 2)(x2 + 2) + 2x(x2 - 2)
= (x2 - 2)(x2 + 2 + 2x)
o) x2(1 - x2) - 4x - 4x2
= x2(1 - x)( 1 + x) - 4x(1 + x)
= x(1 + x)[x(1 - x) - 4x]
= x(x + 1)(x - x2 - 4)
p) x3 + y3 + z3 - 3xyz
= x3 + y3 + z3 - 3x2y + 3x2y - 3xy2 + 3xy2 - 3xyz
= [(x3 + 3x2y + 3xy2 + y3) + z3] - (3x2y + 3xy2 + 3xyz)
= [(x + y)3 + z3] - 3xy(x + y + z)
= (x + y + z)[(x + y)2 - (x + y)z + z2] - 3xy(x + y + z)
= (x + y + z)(x2 + 2xy + y2 - xz - yz + z2 - 3xy)
= (x + y + z)(x2 + y2 + z2 - xy - xz - yz)
q) (x - y)3 + (y - z)3 + (z - x)3
= [(x - y) + (y - z)][(x - y)2 - (x - y)(y - z) + (y - z)2] + (z - x)3
= (x - z)(x2 - 2xy + y2 - xy + xz - y2 + yz + y2 - 2yz + z2) - (x - z)3
= (x - z)(x2 + y2 + z2 - 3xy + xz - yz) - (x - z)3
= (x - z)[x2 + y2 + z2 - 3xy + xz - yz - (x - z)2]
= (x - z)(x2 + y2 - 3xy + xz - yz - x2 + 2xz - z2)
= (x - z)(y2 - 3xy + 3xz - yz)
= (x - z)[(y2 - yz) - (3xy - 3xz)]
= (x - z)[y(y - z) - 3x(y - z)
= (x - z)(y - 3x)(y - z)
Nhớ tik nha

a)\(2x^2-7xy+5y^2\)
\(=2x^2-2xy-5xy+5y^2\)
\(=2x\left(x-y\right)-5y\left(x-y\right)\)
\(=\left(x-y\right)\left(2x-5y\right)\)
b)\(x^3+3x^2y-4xy^2-12y^3\)
\(=\left(x^3+3x^2y\right)-\left(4xy^2+12y^3\right)\)
\(=x^2\left(x+3y\right)-4y^2\left(x+3y\right)\)
\(=\left(x+3y\right)\left(x^2-4y^2\right)\)
\(=\left(x+3y\right)\left(x-2y\right)\left(x+2y\right)\)

23.27. \(x^2-y^2-2x+1\)
\(=\left(x-1\right)^2-y^2\)
\(=\left(x-1-y\right)\left(x-1+y\right)\)
23.25.
\(\left(x^2-4x\right)^2+\left(x-2\right)^2-10\)
\(=\left(x^2-4x\right)^2-4+\left(x-2\right)^2-6\)
\(=\left(x^2-4x+4\right)\left(x^2-4x-4\right)+x^2-4x+4-6\)
\(=\left(x^2-4x+4\right)\left(x^2-4x-10\right)\)
23.23
\(x^3-2x^2-6x+27\)
\(=\left(x^3+27\right)-2x\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2-3x+9-2x\right)\)
\(=\left(x+3\right)\left(x^2-5x+9\right)\)
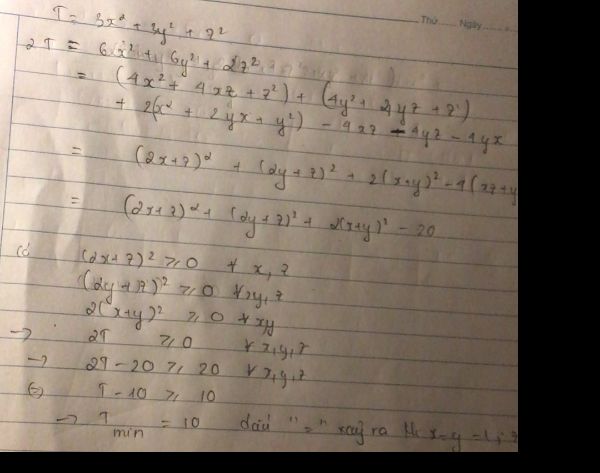




 giai ho mk vs
giai ho mk vs

 Bạn nào giải giúp mình vs
Bạn nào giải giúp mình vs






 Giúp e với ạ
Giúp e với ạ giúp e với ạ
giúp e với ạ

 Giúp vs æ! Cho like ạ! Trong hình là đề ạ! Giúp vs cần gấp lắm! Mơn anh chị!
Giúp vs æ! Cho like ạ! Trong hình là đề ạ! Giúp vs cần gấp lắm! Mơn anh chị!