Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: \(x=10cos\left(5\pi\cdot\dfrac{1}{15}+\dfrac{\pi}{3}\right)=-5\\ v=x'=-50\pi sin\left(5\pi\cdot\dfrac{1}{15}+\dfrac{\pi}{3}\right)=-25\pi\sqrt{3}\)
Phương trình: \(x=2cos\left(5\pi t-\dfrac{\pi}{4}\right)\)
a)Biên độ: \(A=2cm\)
Chu kì: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)
Chiều dài quỹ đạo: \(L=2A=2\cdot2=4cm\)
b)Phương trình chất điểm:
Vận tốc: \(v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi sin\left(5\pi t-\dfrac{\pi}{4}\right)\)
Gia tốc: \(a=-\omega^2Acos\left(\omega t+\varphi\right)=-500cos\left(5\pi t-\dfrac{\pi}{4}\right)\)
c)Em thay giá trị \(t=0,2s\) vào từng pt nhé.
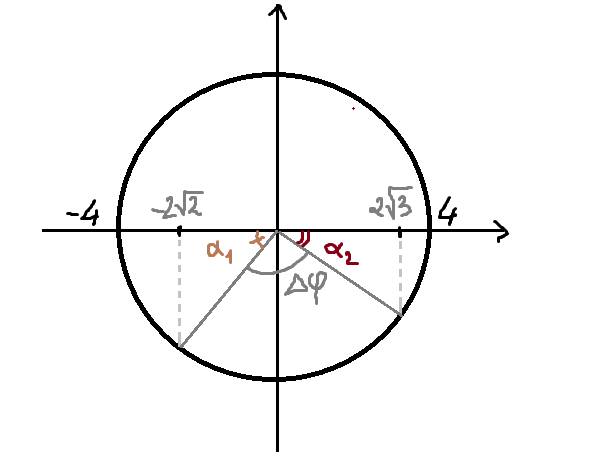
Ta có : \(A=4cm\)
\(cos\alpha_1=\dfrac{-2\sqrt{2}}{4}=-\dfrac{\sqrt{2}}{2}\Rightarrow\alpha_1=\dfrac{3\pi}{4}rad\)
\(cos\alpha_2=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\Rightarrow\alpha_2=\dfrac{\pi}{6}rad\)
\(\Delta\varphi=\left(\dfrac{\pi}{2}-\dfrac{3\pi}{4}\right)+\left(\dfrac{\pi}{2}-\dfrac{\pi}{6}\right)=\dfrac{\pi}{12}rad\)
Có : \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2s\)
\(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{\pi}{12}}{2\pi}.2=\dfrac{1}{12}s\)
Vậy ...
Hình ảnh biểu diễn :
\(L=12cm\Rightarrow A=\dfrac{L}{2}=6cm\)
Chu kì dao động: \(T=\dfrac{62,8}{20}=3,14s\approx\pi\left(s\right)\Rightarrow\omega=\dfrac{2\pi}{T}=2\)
Áp dụng pt độc lập: \(x^2+\dfrac{v^2}{\omega^2}=A^2\)
\(\Rightarrow\left(-2\right)^2+\dfrac{v^2}{2^2}=6^2\Rightarrow v=\pm8\sqrt{2}\left(cm/s\right)=\pm0,08\sqrt{2}\left(m/s\right)\)
Mà vật đang chuyển động the chiều dương: \(v=0,08\sqrt{2}\left(m/s\right)\)
Gia tốc vật:
\(a=-\omega^2x=-2^2\cdot\left(-2\right)=8cm/s^2\)
