Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
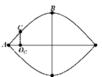
![]() . Chọn nút A làm gốc.
. Chọn nút A làm gốc.
![]()
![]()
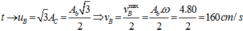
Chú ý: Khi thay đổi tần số sóng từ tần số thấp đến tần số cao thì số bó sóng xuất hiện tăng dần sau đó ổn định. Số lần sóng dừng xuất hiện trên dây tương ứng với số bó sóng.

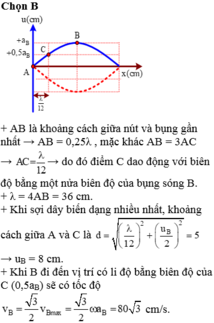
Đáp án B
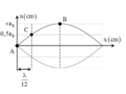
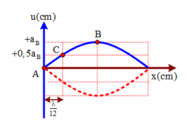
+ AB là khoảng cách giữa nút và gần bụng nhất ⇒ A B = λ 4
Mặt khác AB=3AC do đó điểm C dao động với biên λ = 4 A B = 36 c m
+ Khi sợi dây biến dạng nhiều nhất, khoảng cách giữa A và C là
d = λ 12 2 + u B 2 2 = 5 ⇒ u B = 8 c m
+ Khi B đi đến vị trí có li độ bằng biên độ của C ( 0 , 5 a B )
v B = 3 2 v B m a x = 3 2 ω a B = 40 3 c m / s

Ta có $\lambda =24cm $
Bạn vẽ hình ra .
Đoạn AB =24cm sau đó vẽ 2 bụng sóng.
Lấy M N nằm giữa sao cho MN= AB/3 = 8 cm.
Khoảng cách MN lớn nhất khi chúng nằm trên bụng và nhỏ nhất khi duỗi thẳng.
Ta có $\dfrac{MN_{lớn}}{MN_{nhỏ}} =1.25 \rightarrow MN_{lớn}=10 \rightarrow $biên độ của M và N là 3cm.
Khoảng cách từ M đến nút bằng 4cm =$\dfrac{\lambda}{6} \rightarrow A_{bụng} =2\sqrt{3}$

Hai điểm có cùng biên độ 2 mm đối xứng nhau qua nút gần nhất và hai điểm có biên độ 3 mm nằm đồi xứng nhau qua bụng gần nhất. Áp dụng công thức tình biên độ điểm, ta có hệ phương trình:
Gọi biên độ sóng tại bụng là 2a.
Ta có : \(\frac{1}{a^2}=\frac{9}{4a^2}=1\rightarrow a=\frac{2}{\sqrt{13}}\)
Xét: \(2a\sin\frac{2\pi x}{\lambda}=2\rightarrow2\lambda=54cm\Rightarrow\lambda=27cm\)
Vậy chọn đáp án A.


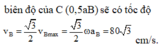

Đáp án C