Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Với mỗi giá trị của x ta có một giá trị xác định của P(x).
Vậy P(x) là một hàm số.
P(x) = x 2
a) Vì AH, HB, AB đều là các đường kính của các nửa đường tròn (O1) , (O2) và (O) nên tứ giác MPHQ có ba góc P, Q, M vuông. Vì vậy nó là hình chữ nhật.
Từ đó, ta có HM = PQ.
b) Vì MHPQ là hình chữ nhật nên \widehat{MPQ}=\widehat{MHQ}=\widehat{MBH}\left(=\dfrac{\stackrel\frown{HQ}}{2}\right)MPQ=MHQ=MBH(=2HQ⌢), do đó APQB là tứ giác nội tiếp.
c) Ta có \widehat{O_1PA}=\widehat{PAO_1}=90^o-\widehat{HMP}=90^o-\widehat{MPQ}O1PA=PAO1=90o−HMP=90o−MPQ
\Rightarrow\widehat{O_1PA}+\widehat{MPQ}=90^o\Rightarrow\widehat{O_1PQ}=90^o⇒O1PA+MPQ=90o⇒O1PQ=90o nên PQ tiếp xúc nửa đường tròn (O1) tại P.
Tương tự , PQ tiếp xúc (O2) tại Q hay PQ là tiếp tuyến chung của hai nửa đường tròn (O1) và (O2)
M A C x B D y H K O I
a) Tam giác AMC vuông tại M có MH là đường cao
\(\Rightarrow MH=\sqrt{AH.BH}\)( hệ thức lượng trong tam giác vuông )
\(\Rightarrow MH=\sqrt{15}\left(cm\right)\)
b) Vì AC song song với BD nên ta có : \(\frac{AC}{BD}=\frac{AI}{ID}=\frac{CM}{MD}\)( vì \(AC=CM;BD=MD\))
\(\Rightarrow MI//AC\)mà \(MH//AC\) ( cùng vuông góc với AB )
Suy ra \(M,I,H\)thẳng hàng
c ) Đặt \(AB=a,AM=c,BM=b\)
Ta có:
\(AK=\frac{a+c-b}{2};BK=\frac{a+b-c}{2}\)
\(\Rightarrow AK.BK=\frac{a+c-b}{2}.\frac{a+b-c}{2}=\frac{1}{2}.\left[\frac{\left(a+c-b\right)\left(a+b-c\right)}{2}\right]\)
\(=\frac{1}{2}\left[\frac{a^2-\left(b-c\right)^2}{2}\right]=\frac{1}{2}\left[\frac{a^2-\left(b^2+c^2\right)+2bc}{2}\right]\)
\(=\frac{1}{2}.\frac{2bc}{2}=\frac{1}{2}.bc=\frac{1}{2}AM.MB=S_{AMB}\)
Vậy \(S_{AMB}=AK.KB\)
Chúc bạn học tốt !!!
Giải:
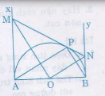
a) Ta có OM, ON lần lượt là tia phân giác cả AOP và BOP
Mà AOP kể bù BOP nên suy ra OM vuông góc với ON.
Vậy ∆MON vuông tại O.
Lại có ∆APB vuông vì có góc vuông (góc nội tiếp chắn nửa cung tròn)
Tứ giác AOPM nội tiếp đường tròn vì có +
= 2v. Nên
=
(cùng chắn cung OP).
Vậy hai tam giác vuông MON à APB đồng dạng vị có cắp góc nhọn bằng nhau.
b)
Tam giác AM = MP, BN = NP (1) (tính chất hai tiếp tuyến cắt nhau)
Tam giác vuông MON có OP là đường cao nên:
MN.PN = OP2 (2)
Từ 1 và 2 suy ra AM.BN = OP2 = R2
c) Từ tam giác MON đồng dạng với tam giác APB ta có :
Khi AM = thi do AM.BN = R2 suy ra BN = 2R
Do đó MN = MP + PN = AM + BN = + 2R =
Suy ra MN2 =
Vậy =
d) Nửa hình tròn APB quay quanh bán kính AB = 2R sinh ra một hình cầu có bán kính R.
Vậy V = πR3
