Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow {g'} =\overrightarrow g - \overrightarrow a \)
Ô tô chuyển động nằm ngang => \(\overrightarrow a \bot \overrightarrow g\)
=> \(g' = \sqrt{g^2+ a^2}\)
\(T = 2\pi \sqrt{\frac{l}{g}}\)
\(T' = 2\pi \sqrt{\frac{l}{g'}}\)
=> \(\frac{T}{T'} = \sqrt{\frac{g'}{g}} = \sqrt{\frac{\sqrt{g^2+a^2}}{g}} = 1,01\)
=> \(T'= \frac{2}{1,01} = 1,98 s.\)
cho mình hỏi: Nếu trong trường hợp ôtô chuyển động thẳng chậm dần đều thì phải làm ntn ?

Khoảng thời gian vận tốc của vật không vượt quá \(6\pi cm/s\) là \(\frac{\Delta t}{T}=\frac{1}{3}\)
\(\Rightarrow\)Góc quét: \(\Delta\varphi=\frac{2\pi}{T}\frac{T}{3}=\frac{2\pi}{3}\left(rad\right)\)
\(\Rightarrow\) VTLG
-v
\(\Rightarrow\cos\varphi=\cos\left(90-30\right)=\frac{v}{v_{max}}=\frac{1}{2}\Rightarrow v_{max}=12\pi=\)\(\omega A\Rightarrow A=3,6cm\)

\(T=2\pi\sqrt{\frac{l}{g}}\)
\(T'=2\pi\sqrt{\frac{l'}{g}}\)
\(\Rightarrow\frac{T'}{T}=\sqrt{\frac{l'}{l}}=\sqrt{2}\Rightarrow T'=2\sqrt{2}s\)

Chọn A
Chu kỳ dao động nhỏ của con lắc đơn khi không có điện trường là
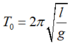
Trường hợp lực điện trường hướng lên (ngược chiều trọng lực):
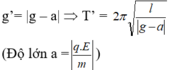
Đổi chiều điện trường:
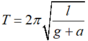
Ta có T’ > T nên theo giả thiết ta được T’ = T2 = 3s, T = T1 = 2s
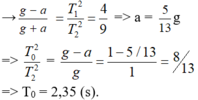

Vì \(T_0< T_1\) , nên E hướng xuống.
Lại có: \(T_1=2T_0\Leftrightarrow2\pi\sqrt{\frac{l}{g-a}}=2.2\pi\sqrt{\frac{l}{g}}\Rightarrow4a=3g\Leftrightarrow a=\frac{3}{4}g\)\(=7,5\left(m/s^2\right)\)
\(a=\frac{qE}{m}\Rightarrow E=\frac{ma}{q}=3,75.10^3\left(V/m\right)\)
Đáp án D

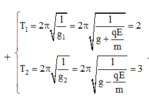
Chu kì của con lắc khi không có điện trường và khi có điện trường hướng thẳng đứng:
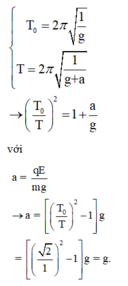
Chu kì của con lắc khi điện trường có hướng hợp với g một góc 60 o
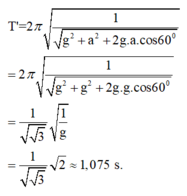
Đáp án A
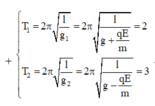
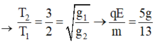
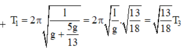
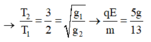
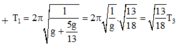

Đáp án C
Vật được tích điện, ở trong điện trường sẽ có lực điện tác dụng lên vật. Nếu lực điện cùng chiều trọng lực, chu kỳ giảm và ngược lại. Theo đề bài, sau khi đổi chiều điện trường thì T tăng, suy ra ban đầu lực điện cùng chiều trọng lực, lúc sau lực điện ngược chiều trọng lực.
Gọi lực điện là F d = m a . Ta có:
T 1 T 2 = g 2 g 1 = g − a g + a = 2 3 ⇒ g = 13 a 5
Suy ra
T T 1 = g 1 g = g + a g = 1 + a g = 1 + 5 13 ⇔ T = 2 , 35 ( s )