
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


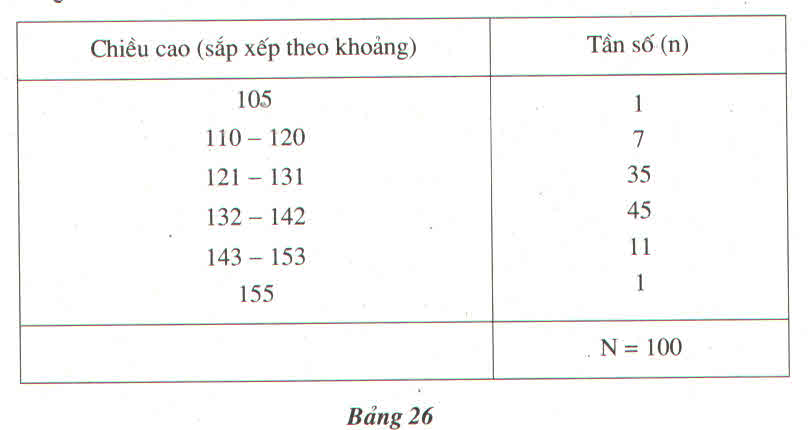
a) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.
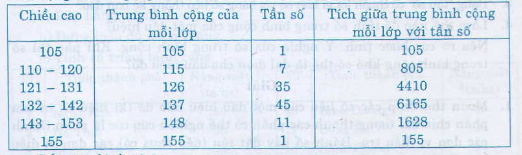
Số trung bình cộng:\(\overline{X}=\dfrac{105+805+4410+6165+1628+155}{100}=132,68\left(cm\right)\)
a) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.

Số trung bình cộng:¯¯¯¯¯X=105+805+4410+6165+1628+155100=132,68(cm)

a) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.

Số trung bình cộng:
\(\overline{X}=\dfrac{105+805+4410+6165+1628+155}{100}=132,68\left(cm\right)\)

Giải:
a) \(-1313x^2y.2xy^3\)
\(=\left(-1313.2\right)\left(x^2.x\right)\left(y.y^3\right)\)
\(=-2626x^3y^4\)
Bậc của đơn thức là: \(3+4=7\)
b) \(1414x^3y.\left(-2x^3y^5\right)\)
\(=\left[1414.\left(-2\right)\right]\left(x^3.x^3\right)\left(y.y^5\right)\)
\(=-2828x^6y^6\)
Bậc của đơn thức là: \(6+6=12\).
Chúc bạn học tốt!!!
a) -x2y. 2xy3 = -2x3y4. Đơn thức có bậc là 7
b) x3y. (-2x3y5) = -2x6y6. Đơn thức có bậc là 12

Theo mình nghĩ thì đề thiếu là tam giác ABC vuông tại A nhé!
Bạn xem lại đề!:)

Hướng dẫn:
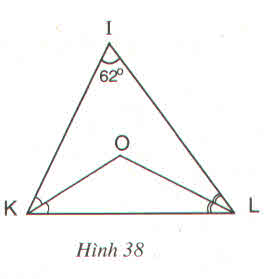
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210

c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
a, Áp dụng định lí tổng 3 góc trong ΔIKL, ta có:
∠I + ∠IKL + ∠ILK= 180 độ
⇒ ∠IKL + ∠ILK= 180 độ - ∠I
OK, OL là phân giác của các góc K, L nên:
∠OKL= 1/2∠IKL, ∠OLK= 1/2∠ILK
⇒ ∠OKL + ∠OLK= 1/2 (∠IKL + ∠ILK)
= 1/2 . (180 độ - ∠I)
Áp dụng định lí tổng 3 góc trong ΔOKL có:
∠ KOL + ∠OKL + ∠OLK = 180 độ
⇒ ∠KOL= 180 độ - (∠OKL + ∠OLK)
= 180 độ - 180- ∠I / 2= 180 + ∠I/2
Mà ∠I= 62 độ nên:
∠KOL= 180 +62/2= 121 độ
b, Ta có: 3 đường phân giác trong tam giác đồng quy.
Mà 2 đường phân giác KO, LO cắt nhau tại O
⇒ OI là tia phân giác của ∠KIL
⇒ ∠KIO= 1/2 ∠KIL= 1/2. 62 độ= 31 độ
c, O là giao điểm 3 đường phân giác của ΔIKL. Áp dụng định lí 3 đường phân giác
Vậy O cách đều 3 cạnh của ΔIKL

\(VT=\dfrac{a+c}{a+b}+\dfrac{b+d}{b+c}+\dfrac{c+a}{c+d}+\dfrac{d+b}{d+a}\)
\(=\left(a+c\right)\left(\dfrac{1}{a+b}+\dfrac{1}{c+d}\right)+\left(b+d\right)\left(\dfrac{1}{b+c}+\dfrac{1}{d+a}\right)\)
Ap dụng \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y} \left(\forall x,y>0\right)\)
Ta có: \(VT\ge\left(a+c\right).\dfrac{4}{a+b+c+d}+\left(b+d\right).\dfrac{4}{a+b+c+d}\)
\(=\dfrac{4\left(a+b+c+d\right)}{\left(a+b+c+d\right)}=4\left(ĐPCM\right)\)

Chọn B