Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Khi L thay đổi thì:
URmax=UCmax ⇔ Cộng hưởng ⇔ Imax = U R => U R m a x = U U C m a x = I m a x Z C = U R Z C
ULmax= U R 2 + Z C 2 R
Theo bài ra: ULmax= 2 URmax hay U R 2 + Z C 2 R = 2U =>ZC = R 2
U L m a x U C m a x = R 2 + Z C 2 Z C = R 2 + 3 R 2 R 3 = 2 3

Điện áp cực đại trên cuộn cảm U C m a x = U Z C R (tương ứng với trường hợp xảy ra cộng hưởng).
Khi xảy ra cực đại trên cuộn dây
U L m a x = 3 U C ⇒ Z L 0 = 3 Z C ⇔ R 2 + Z C 2 Z C = 3 Z C .
→ Tiến hành chuẩn hóa R = 1
→ 1 + Z C 2 Z C = 3 Z C → S h i f t → S o l v e Z C = 2 2 .
→ Tỉ số U L m a x U C m a x = R 2 + Z C 2 Z C = 1 2 + 2 2 2 2 2 = 3 .
Đáp án C

Điện áp cực đại trên cuộn cảm U L m a x = U R 2 + Z C 2 R = 90 2 V .
Đáp án D

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

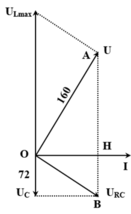
Khi điện áp hiệu dụng ở hai đầu cuộn dây cực đại thì u vuông pha với u R C → U R C = U L m a x 2 − U 2 = 3 U = 3 (chuẩn hóa U = 1).
Mặc khác U R U L m a x = U U R C ⇒ U R = U U R C U L m a x = 3 2
→ Hệ số công suất của mạch khi bỏ cuộn dây cos φ = U R U R C = 1 2
Đáp án A
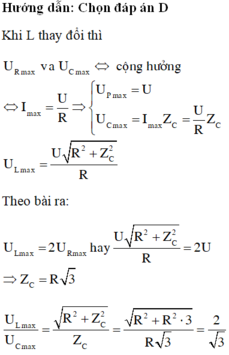



Khi L thay đổi thì: URmax và UCmax \(\leftrightarrow\) cộng hưởng \(\leftrightarrow\) \(\begin{cases}I_{max}=\frac{U}{R}\rightarrow\begin{cases}U_{Rmax}=U\\U_{Cmax}=I_{max}.Z_C=\frac{U}{R}.Z_C\end{cases}\\U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}\end{cases}\)
Theo đề bài: \(U_{Lmax}=2U_{Rmax}\) hay
\(\begin{cases}\frac{U\sqrt{R^2+Z^2_C}}{R}=2U\rightarrow Z_C=R\sqrt{3}\\\frac{U_{Lmax}}{U_{Cmax}}=\frac{\frac{U\sqrt{R^2+Z^2_C}}{R}}{\frac{U}{R}.Z_C}=\frac{\sqrt{R^2+Z^2_C}}{Z_C}\end{cases}\)\(\rightarrow\frac{U_{Lmax}}{U_{Cmax}}=\frac{\sqrt{R^2+\left(R\sqrt{3}\right)^2}}{R\sqrt{3}}=2\sqrt{3}\)
chọn D
ai zúp mk zới