Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tui hok lớp 6 chắc phải gọi bà là cj rùi mà tui cx k bt về lớp 11 .Sorry nhen!!![]()

Công suất tiêu thụ ở mạch ngoài là: \(P=I^2.R=(\dfrac{E}{R+r})^2.R\)
\(\Rightarrow 4=(\dfrac{6}{R+2})^2.R\)
\(\Rightarrow R^2+4R+4=9R\)
\(\Rightarrow R^2-5R+4=0\)
Giải phương trình ta tìm được:
\(R_1=1\Omega\)
\(R_2=4\Omega\)

Công suất trên điện trở R:
\(P=I^2\cdot R=\dfrac{\xi^2}{\left(R+10+10\right)^2}\cdot R=\dfrac{\xi^2}{\left(R+25\right)^2}R\)
\(P_{max}\Leftrightarrow\left(R+25\right)^2min\)
Áp dụng bđt Cô-si ta có:
\(R+25\ge2\cdot\sqrt{25R}=10\sqrt{R}\)
Dấu \("="\) xảy ra\(\Leftrightarrow a=b\Rightarrow R=25\Omega\)
Vậy \(x=R=25\Omega\)
Bạn nguyễn thị hương giang ơi, bạn có thể giải thích cho mình dòng đầu tiên được không? Cảm ơn bạn nhiều <3 <3 <3

a) Để công suất tiêu thụ mạch ngoài là lớn nhất thì R+X=r
=> X=1,1 - 0,1=1(\(\Omega\)
b) Để công suất tiêu thụ ở điện trở này là lớn nhất thì X=R+r =1,1+0,1=1,2\(\Omega\)
Công suất đó là: Pmax =I2.R=\(\left(\frac{\in}{R+X+r}\right)^2.X=\left(\frac{12}{1,1+1,2+0,1}\right)^2.1,2=30\left(\text{W}\right)\)

a) Tính điện trở x để công suất tiêu thụ ở mạch ngoài là lớn nhất.
- Mạch ngoài gồm điện trở R mắc nối tiếp với điện trở x, có điện trở tương đương là: RN = R + x = 0,1 + x.
- Cường độ dòng điện trong trong mạch : I = ξ/ (R + r + x)
- Công suất tiêu thụ mạch ngoài:

Để công suất P trên đây lớn nhất thì mẫu số ở về phải là nhỏ nhát. từ bất đẳng thức cô si ta có R + x = r.
Từ đó suy ra: x = r –R = 1 Ω.
b) Công suất tiêu thụ trên điện trở x:
- Tính công suất tiêu thụ trên điện trở x này là lớn nhất:
+ Từ các tính toán trên, ta có công suất tiêu thu, điện trở x là:
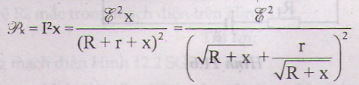
+ Tương tự như đã làm ở trên đây, công suất Px lớn nhất khi x= R + r = 1,2 Ω.
Giá trị của công suất lớn nhất này là:30 W.


a) Tìm công suất tỏa nhiệt trên điện trở R 4
Chọn chiều dòng điện qua các điện trở trong mạch như hình vẽ.
* Xét tại nút A ta có: I = I 1 + I 2 (1)
Với vòng kín ACDA ta có:
I 1 R 1 - I X R X - I 2 R 2 = 0 (2)
Thế (1) vào (2) ta được biểu thức I :
I 1 R 1 - I X R X - ( I - I 1 ) R 2 = 0 I 1 R 1 - I X R X - I R 2 + I 1 R 2 = 0 I 1 ( R 1 + R 2 ) = I X R X + I R 2 ⇒ I 1 = I X . R X + I . R 2 R 1 + R 2 = I X . R X + I . R 4 R (3)
* Xét tại nút B ta có: I 3 = I - I 4 (4)
Với vòng kín BCDB ta có:
I 3 R 3 - I X R X + I 4 R 4 = 0 I 3 R - I X R X + I 4 X = 0 (5)
Thế (4) vào (5) ta có biểu thức I 4 :
( I - I 4 ) R - I X R X + I 4 R = 0 I . R + I 4 R - I X R X + I 4 R = 0
⇒ I 4 = I . R + I X R X 2 R (6)
Từ (3) và (6) ta có: = 2 ð = =
Vậy công suất tỏa nhiệt trên R 4 khi đó là P 4 = 4 3 P 1 = 12 W .
b) Tìm R X theo R để công suất tỏa nhiệt trên R X cực đại
Từ (4) và (5) ta có biểu thức I 3 :
I 3 R - I X R X + ( I - I 3 ) R = 0 I 3 R - I X R X + I R - I 3 R = 0 ⇒ I 3 = I . R - I X R X 2 R (7)
Ta có: U = U A B = U A C + U C B = I 1 . R 1 + I 3 R 3 U = I 1 3 R + I 3 R (8)
Thế (3) và (7) vào (8) ta được:
U = I X R X + I . R 4 R . 3 R + I . R - I X R X 2 R . R 4 U = 3 . I X R X + 3 . I . R + 2 I . R - 2 I X R X 4 U = 5 . I . R + I X R X (9)
Tính I:
Ta có:
I = I 1 + I 2 = I 1 + I 4 + I X = 3 I 1 + I X = 3 . I X R X + I R 4 R + I X ⇒ 4 . I . R = 3 I X R X + 3 . I . R +...