Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

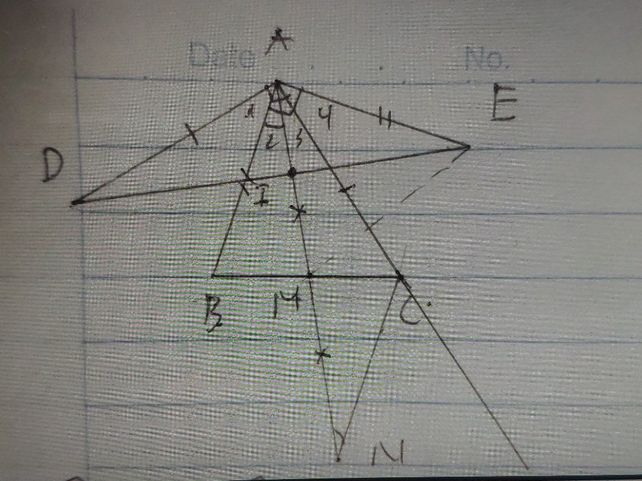
tu ve hinh :
a, AE | AB va AD | AC (gt) => goc DAC = goc BAE = 90 (dn)
goc DAB + goc BAC = goc DAC
goc EAC + goc CAB = goc BAE
=> goc DAB = goc CAE
xet tamgiac BDA va tamgiac ECA co :
AD = AC (gt) va AB = AE (gt)
=> tamgiac BDA = tamgiac ECA (c - g - c)
=> BD = CE (dn)

a/ Xét tg ABM và tg ACM có
AB = AC ( gt)
BM = CM ( gt)
AM chung
=> tg ABM = tg ACM (ccc)
b/ ( Trên tia đối của tia MA chứ ko phải AM nha )
Xét tg AMC và tg DMB, có
MC = MB (gt)
AM = MD ( gt)
^AMC = ^BMD ( đđ )
=> tg AMC = tg DMB ( cgc)
=> AC = BD
c/ tg ABC cân tại A có AM là đường trung tuyến
=> AM cũng là đường cao
=> AD vuông góc BC (1)
Lại có AM = MD , BM = MC ( gt) (2)
Từ (1), (2) => ABCD là hình thoi
=> AB // CD
d/ Theo đề : AI // BC , AI = BC
=> ABCI là hình bình hành
=> AB // CI
Mà AB // BC ( cmt )
=> I , C ,D thẳng hàng