Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

â)vì tam giác bcd nội tiếp (ô) đường kính bd nên tam giác bcd vuông
b)xet (o) co :oh vuong goc bd tai h nen h la trung diem bc(tc) xet tam giac abc co ah la duong cao(gt) va la duong trung tuyen(cmt) nen tam giac abc can tai a nen goc bah=cah va ab=ac nen tam giac bao=tam giac cao nen goc oba=oca suy ra oca=90 do suy ra dpcm

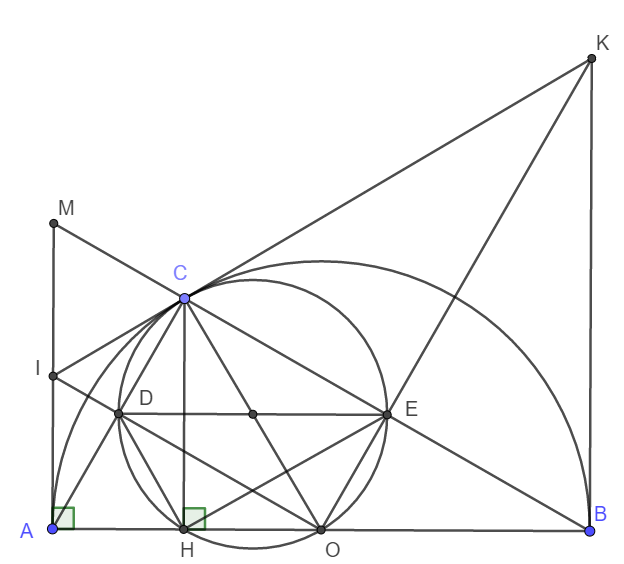
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.

a, Ta có : góc ABC = góc CDB ( = 1/2 sđ cung BC nhỏ )
=> tam giác ABC đồng dạng với tam giác ADB (g.g)
=> AB/AD = AC/AB
=> AB^2 = AC.AD
Tk mk nha


1) Do B, C cùng thuộc đường tròn đường kính AO nên \(\widehat{ABO}=\widehat{ACO}=90^o\) (Góc nội tiếp chắn nửa đường tròn)
Vậy nên AB, AC là các tiếp tuyến của đường tròn (O).
Xét tam giác vuông ABO có \(AO=R\sqrt{2};OB=R\)
Áp dụng định lý Pi-ta-go ta có:
\(AB=\sqrt{AO^2-BO^2}=R\)
Vậy thì AC = AB = R.
2) Ta thấy tứ giác ABOC có AB = BO = OC = CA = R nên nó là hình thoi.
Lại có \(\widehat{ABO}=90^o\) nên ABOC là hình vuông.
3) Xét tam giác ADC và tam gác ACE có:
Góc A chung
\(\widehat{ACD}=\widehat{AEC}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn cung DC)
\(\Rightarrow\Delta ADC\sim\Delta ACE\left(g-g\right)\)
\(\Rightarrow\frac{AD}{AC}=\frac{AC}{AE}\Leftrightarrow AD.AE=AC^2=R^2\) = hằng số.
Hoàn toàn tương tự ta cũng có AM.AN = AB2 = R2 = hằng số.
Vậy nên AM.AN = AD.AE = R2.
4) Xét đường tròn (O), ta có K là trung điểm dây cung MN nên theo liên hệ đường kính dây cung, ta có: \(OK\perp MN\) hay \(\widehat{AKO}=90^o\)
Vậy thì K thuộc đường tròn đường kính OA.
Do AMN là cát tuyến nên K thuộc cung tròn BmC (trên hình vẽ).
5) Ta có ABOC là hình vuông nên AO và BC cắt nhau tại trung điểm mỗi đường.
Vậy thì BC qua tâm I.
Từ đó ta có \(\widehat{IJO}=90^o\)
Lại vừa chứng minh được \(\widehat{JKO}=90^o\).
Tứ giác IJKO có tổng hai góc đối bằng 180o nên IJKO là tứ giác nội tiếp hay O, K, I, J cùng thuộc một đường tròn.
Ta có AB = AC nên \(\widebat{AB}=\widebat{AC}\Rightarrow\widehat{BKA}=\widehat{CBA}=\widehat{JBA}\)
Vậy thì \(\Delta ABJ\sim\Delta AKB\left(g-g\right)\Rightarrow\frac{AB}{AK}=\frac{AJ}{AB}\Rightarrow AJ.AK=AB^2\)


a gọi I là trung điểm của A=> I thuộc đường tròn (O) vì OI-1/2.)OA=1.2.2R=R= BK
có AB,AC là tiếp tuyến của (O)
=>góc ABO=góc ACO=90 độ
=> tam giác ABO vuông tại B, có BI là đường trung tuyến
=> BI=OI=IA
có OI=OC=OB
=> tứ giác OBIC là hình thoi
=> OI là đường phân giác của góc BIC(tính chất hình thoi) hay AI là phân giác góc BAC(1)
lại có ABOC nội tiếp(O) (cmt)
=> AO vuông góc với BC hay AI vuông góc với BC(2), AB=AC(3)
từ (1)(2)(3)=> tam giác ABC đều
O A B C D E
a) Ta thấy ngay \(\widehat{BDA}=\widehat{CBA}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cung cùng chắn một cung)
Vậy nên \(\Delta ABC\sim\Delta ADB\left(g-g\right)\)
b) Do \(\Delta ABC\sim\Delta ADB\Rightarrow\frac{AB}{AD}=\frac{AC}{AB}\Rightarrow AB^2=AD.AC\)
Xét tam giác vuông OBA có \(AB=\sqrt{AO^2-OB^2}=\sqrt{4R^2-R^2}=R\sqrt{3}\)
Vậy nên \(AD.AC=AB^2=3R^2\)
c) Ta thấy rằng \(\Delta ABC\sim\Delta ADB\Rightarrow\widehat{ABC}=\widehat{ADB}\)
Vậy thì \(\widehat{BEA}=\widehat{DBE}+\widehat{BDE}=\widehat{ABC}+\widehat{CBE}=\widehat{ABE}\)
Suy ra tam giác ABE cân tại A hay AB = AE.
Do A, B cố định nên AE không đổi.
Vậy khi cát tuyến ACD quay xung quanh A thì E di chuyển trên đường tròn tâm A, bán kính AB.
d) Ta có AC.AD = 3R2 ; AC + AD = 7R/2
nên ta có phương trình \(AC\left(\frac{7R}{2}-AC\right)=3R^2\)
\(\Leftrightarrow AC^2-\frac{7R}{2}AC+3R^2=0\Leftrightarrow AC=2R\)
\(\Rightarrow AD=\frac{3R}{2}\)