Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A A B D C H N M
Ta cần chứng minh \(\overrightarrow{MN}.\overrightarrow{AM}=0\)
Đặt \(\frac{BM}{MH}=\frac{CN}{ND}=k\), khi đó \(\overrightarrow{MB=}-k\overrightarrow{MH}\) , \(\overrightarrow{NC=}-k\overrightarrow{ND}\)
Suy ra \(\left(1+k\right)\overrightarrow{AM}=\overrightarrow{AB}+k\overrightarrow{AH}\)
và \(\left(1+k\right)\overrightarrow{MN}=\overrightarrow{BC}+k\overrightarrow{HD}\)
Suy ra :
\(\left(1+k\right)^2\overrightarrow{MN}.\overrightarrow{AM}=k\left(\overrightarrow{AB}.\overrightarrow{HD}+\overrightarrow{AH}.\overrightarrow{BC}\right)\)
\(=k\left(\overrightarrow{HB}.\overrightarrow{HD}+\overrightarrow{AH}.\overrightarrow{BC}\right)\)
\(=k\left(\overrightarrow{-AH^2}+\overrightarrow{AH}.\overrightarrow{AD}\right)\)
\(=k\overrightarrow{AH}.\overrightarrow{HD}=0\)
Suy ra điều phải chứng minh

Đặt : \(\overrightarrow{BA}=\overrightarrow{a},\overrightarrow{BB'}=\overrightarrow{b,}\overrightarrow{BC}=\overrightarrow{c}\)
Ta có : \(\overrightarrow{BD'}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
Do MM//BD' nên tồn tại số thực k sao cho \(\overrightarrow{MN}=k\overrightarrow{BD'}\)
hay :
\(\overrightarrow{MN}=k\overrightarrow{a}+k\overrightarrow{b}+k\overrightarrow{c}\) (1)
Đặt
\(\frac{MC}{AC}=x,\frac{C'N}{C'D}=y;x,y\in\left(0;1\right)\)
Ta có :
\(\overrightarrow{AC}=\overrightarrow{c}-\overrightarrow{a,}\overrightarrow{C'D}=\overrightarrow{a}-\overrightarrow{b,}\)
Suy ra : \(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CC'}+\overrightarrow{C'N}\)
\(=\overrightarrow{xAC}+\overrightarrow{CC'}+\overrightarrow{yC'N}\)
\(=x\left(\overrightarrow{c}-\overrightarrow{a}\right)+\overrightarrow{b}+y\left(\overrightarrow{a}-\overrightarrow{b}\right)\)
\(=\left(y-x\right)\overrightarrow{a}+\left(1-y\right)\overrightarrow{b}+x\overrightarrow{c}\) (2)
Từ (1) và (2) suy ra :
\(k\overrightarrow{a}+k\overrightarrow{b}+k\overrightarrow{c}=\left(y-x\right)\overrightarrow{a}+\left(1-y\right)\overrightarrow{b}+x\overrightarrow{c}\)
\(\Leftrightarrow\left(k+x-y\right)\overrightarrow{a}+\left(k+y-1\right)\overrightarrow{b}+\left(k-x\right)\overrightarrow{c}=\overrightarrow{0}\) (3)
Do \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) không đồng phửng nên (3) tương đương với
\(\begin{cases}k+x-y=0\\k+y-1=0\\k-x=0\end{cases}\) \(\Leftrightarrow\begin{cases}x=\frac{1}{3}=k\\y=\frac{2}{3}\end{cases}\)
Vậy với \(3\overrightarrow{MC}=\overrightarrow{AC,}3\overrightarrow{C'N}=2\overrightarrow{C'D}\)
thì MN//BD' và khi đó \(\frac{MN}{BD'}=\frac{1}{3}\)
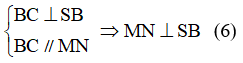


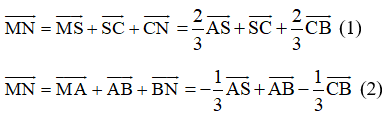
C' C B N B' D' A' A D M b a
Đặt \(\overrightarrow{AB}=\overrightarrow{a}\) , \(\overrightarrow{AD}=\overrightarrow{b}\) ,\(\overrightarrow{AA'}=\overrightarrow{c}\)
Với \(\begin{cases}\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|=1\\\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=0\end{cases}\)
Suy ra \(\overrightarrow{A'C}=\overrightarrow{AC}-\overrightarrow{AA'}=\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\)
Từ giả thiết suy ra \(\frac{AM}{AD}=\frac{B'N}{B'B}\)
Do đó
\(\overrightarrow{AM}=k.\overrightarrow{b}\) , \(\overrightarrow{AN}=\overrightarrow{a}+\left(1-k\right).\overrightarrow{c}\)
Ở đây, \(k=\frac{AM}{AD}=\frac{B'N}{B'B}\)
Suy ra :
\(\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}=\overrightarrow{a}-k.\overrightarrow{b}+\left(1-k\right).\overrightarrow{c}\)
Khi đó :
\(\overrightarrow{MN}.\overrightarrow{A'C}=\left(\overrightarrow{a}-k.\overrightarrow{b}+\left(1-k\right).\overrightarrow{c}\right).\left(\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\right)\)
\(=1-k+k-1=0\)
Do đó : \(MN\perp A'C\)