Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B và D giống nhau nên chắc chắn cả 2 đều đúng
Kiểm tra 2 đáp án A và C:
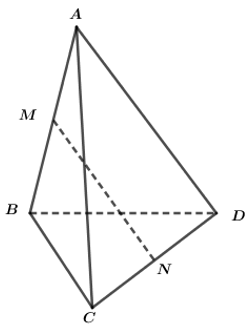
\(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{MC}+\overrightarrow{MD}\right)=\frac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{AC}+\overrightarrow{MB}+\overrightarrow{BD}\right)=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{BD}\right)\)
Vậy đáp án A đúng nên đáp án C sai

1/ \(\overrightarrow{AB}^2-\overrightarrow{AD}^2=\overrightarrow{BC}^2-\overrightarrow{CD}^2\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{AB}-\overrightarrow{AD}\right)=\left(\overrightarrow{BC}+\overrightarrow{CD}\right)\left(\overrightarrow{BC}-\overrightarrow{CD}\right)\)
\(\Leftrightarrow\left(\overrightarrow{AB}+\overrightarrow{AD}\right).\overrightarrow{DB}=\overrightarrow{BD}\left(\overrightarrow{BC}-\overrightarrow{CD}\right)=\overrightarrow{DB}\left(\overrightarrow{CB}+\overrightarrow{CD}\right)\)
Gọi M là trung điểm BD
\(\Rightarrow2\overrightarrow{AM}.\overrightarrow{DB}=2\overrightarrow{CM}.\overrightarrow{DB}\)
\(\Leftrightarrow\overrightarrow{DB}.\left(\overrightarrow{AM}-\overrightarrow{CM}\right)=0\)
\(\Leftrightarrow\overrightarrow{BD}.\overrightarrow{AC}=0\)
2/ \(A=\left|\overrightarrow{a}-\overrightarrow{b}\right|\Rightarrow A^2=\overrightarrow{a}^2-2\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}^2\)
\(=a^2+b^2-2ab.cos\left(\overrightarrow{a};\overrightarrow{b}\right)=4^2+5^2-2.4.5.cos120^0=61\)
\(\Rightarrow A=\sqrt{61}\)
b/ \(B=\left|2\overrightarrow{a}+\overrightarrow{b}\right|\Rightarrow B^2=4a^2+b^2+4\overrightarrow{a}.\overrightarrow{b}\)
\(=4a^2+b^2+4ab.cos120^0=49\)
\(\Rightarrow B=7\)
3/ \(\left|\overrightarrow{x}\right|=\left|\overrightarrow{a}-2\overrightarrow{b}\right|\Rightarrow\left|\overrightarrow{x}\right|^2=a^2+4b^2-4\overrightarrow{a}.\overrightarrow{b}=12\)
\(\Rightarrow\left|\overrightarrow{x}\right|=2\sqrt{3}\)
\(\left|\overrightarrow{y}\right|^2=a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=5\Rightarrow\left|\overrightarrow{y}\right|=\sqrt{5}\)
\(\overrightarrow{x}.\overrightarrow{y}=\left(\overrightarrow{a}-2\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)=a^2+2b^2-3\overrightarrow{a}.\overrightarrow{b}=4\)
\(\Rightarrow cos\alpha=\frac{\overrightarrow{x}.\overrightarrow{y}}{\left|\overrightarrow{x}\right|.\left|\overrightarrow{y}\right|}=\frac{4}{2\sqrt{15}}=\frac{2\sqrt{15}}{15}\)

Phương trình dạng tổng quát của \(d_1\): \(x+3y-7=0\)
Phương trình dạng tổng quát của \(d_2\): \(x-3y+2=0\)
a/ Gọi M là 1 điểm bất kì thuộc \(d_1\Rightarrow x_M+3y_M-7=0\) (1)
Gọi M' là ảnh của M qua phép tịnh tiến \(\overrightarrow{a}\Rightarrow\left\{{}\begin{matrix}x_M=x_{M'}-1\\y_M=y_{M'}-1\end{matrix}\right.\)
Thay vào (1): \(x_{M'}-1+3\left(y_{M'}-1\right)-7=0\)
\(\Leftrightarrow x_{M'}+3y_{M'}-11=0\)
Vậy ảnh của \(d_1\) có pt: \(x+3y-11=0\)
Gọi \(M_2\) là 1 điểm bất kì thuộc \(d_2\Rightarrow x_{M_2}-3y_{M_2}+2=0\)
Gọi M'' là ảnh của \(M_2\) qua phép tịnh tiến \(\overrightarrow{a}\) \(\Rightarrow\left\{{}\begin{matrix}x_{M2}=x_{M''}-1\\y_{M2}=y_{M''}-1\end{matrix}\right.\)
\(\Rightarrow x_{M''}-1-3\left(y_{M''}-1\right)+2=0\Leftrightarrow x_{M''}-3y_{M''}+4=0\)
Ảnh của d2 là: \(x-3y+4=0\)
b/ \(\Rightarrow I\left(5;-6\right)\)
Gọi M là 1 điểm bất kì thuộc d \(\Rightarrow4x_M-2y_M+3=0\) (1)
Gọi M' là ảnh của M qua phép đối xứng tâm I
\(\Rightarrow\left\{{}\begin{matrix}x_M=10-x_{M'}\\y_M=-12-y_{M'}\end{matrix}\right.\)
Thế vào (1): \(4\left(10-x_{M'}\right)-2\left(-12-y_{M'}\right)+3=0\)
\(\Rightarrow4x_{M'}-2y_{M'}-67=0\)
Hay ảnh của d qua phép đối xứng tâm I có pt: \(4x-2y+67=0\)
- Tương tự, gọi \(M_1\) là 1 điểm bất kì thuộc \(d_1\Rightarrow x_{M1}+3y_{M1}-7=0\)
\(M_1'\) là ảnh của M qua phép đối xứng tâm I \(\Rightarrow\left\{{}\begin{matrix}x_{M1}=10-x_{M_1'}\\y_{M1}=-12-y_{M_1'}\end{matrix}\right.\)
\(\Rightarrow10-x_{M_1'}+3\left(-12-y_{M_1'}\right)-7=0\)
\(\Leftrightarrow x_{M_1'}+3y_{M_1'}+33=0\)
Ảnh của d1 là: \(x+3y+33=0\)
Ảnh của d2 bạn tự làm nốt tương tự


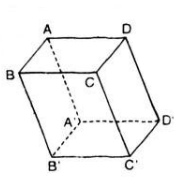

Sửa xíu: \(\overrightarrow{AM}=k\overrightarrow{AC'}\)