Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

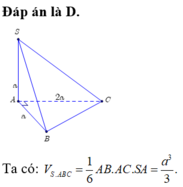
Đáp án là D
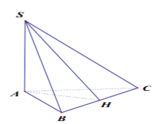
Gọi H là trung điểm của BC, ta có: AH ⊥ BC
Do SA
⊥
(ABC) ![]()
Ta có: ![]()
Xét tam giác vuông SAH:
![]()
![]()

Đáp án B
HDG:
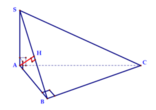
![]()
Dễ dàng chứng minh ∆ S B C vuông tại B
![]()
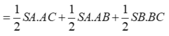
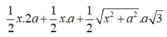
![]()
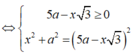
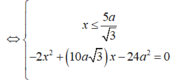
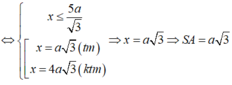
Ta có (SAB) ⊥ (SBC) theo giao tuyến SB. Kẻ
![]()
![]()

Đáp án B
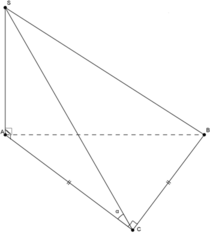
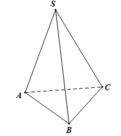
Ta có BC ⊥ AC và BC ⊥ SC, do đó góc giữa mp (SBC) và mp (ABC) chính là góc SCA.
Mặt khác
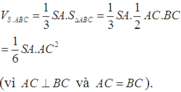
Vì tam giác SAC vuông tại A nên ta có
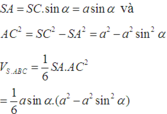
đặt t = sin α ta có hàm số thể tích theo t như sau
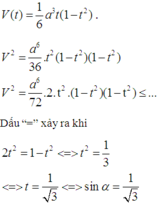

Chọn đáp án D
+ Gọi H là trung điểm SB. Do tam giác SAB vuông tại A, SBC vuông tại C suy ta HA = HB = HS = HC
Suy ra H là tâm mặt cầu.
+ Gọi I là hình chiếu của H lên (ABC). Do HA = HB = HC , suy ra IA = IB = IC
Suy ra I là trung điểm AC. Gọi P là trung điểm BC, do tam giác ABC vuông cân, suy ra
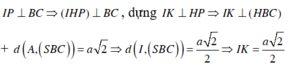
Áp dụng hệ thức
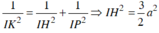
\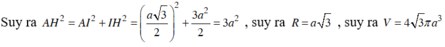
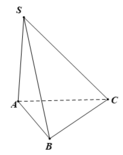
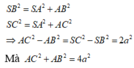
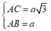
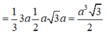
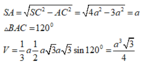
Đáp án B
Gọi M là trung điểm của BC. Vì ∆ ABC cân tại A nên AM ⊥ BC,
Ta có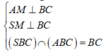
=> Góc giữa (SBC) và (ABC) là góc SMA. Vì góc SAM = 90 0
Có BM = a, góc BAM = 60 0 nên