TD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 4 2016
a) Tập xác định : D = R { 1 }.
> 0, ∀x
1.
Hàm số đồng biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
b) Tập xác định : D = R { 1 }.
< 0, ∀x
1.
Hàm số nghịch biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
c) Tập xác định : D = (-∞ ; -4] ∪ [5 ; +∞).
∀x ∈ (-∞ ; -4] ∪ [5 ; +∞).
Với x ∈ (-∞ ; -4) thì y’ < 0; với x ∈ (5 ; +∞) thì y’ > 0. Vậy hàm số nghịch biến trên khoảng (-∞ ; -4) và đồng biến trên khoảng (5 ; +∞).
d) Tập xác định : D = R { -3 ; 3 }.
< 0, ∀x
±3.
Hàm số nghịch biến trên các khoảng : (-∞ ; -3), (-3 ; 3), (3 ; +∞).
DH
0
1 tháng 4 2016
Tập xác định : D = R. y' = => y' = 0 ⇔ x=-1 hoặc x=1.
Bảng biến thiên :
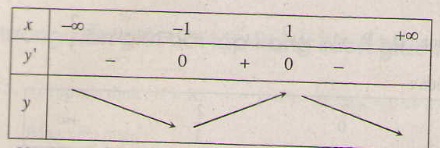
Vậy hàm số đồng biến trên khoảng (-1 ; 1); nghịch biến trên các khoảng (-∞ ; -1), (1 ; +∞).
NH
5
25 tháng 3 2016
a+3c=8 nên c=(8-a)/3
a+2b=9 nên b=(9-a)/2
=>a+3c+a+2b=8+9
2a+2b+2c+c=17
2(a+b+c)=17+c
2[a+(9-a)/2+(8-a)/3]=17+(8-a)/3
2[6a/6+(27-3a)/6+(16-2a)/6]=17+(8-a)/3
2[(6a+27-3a+16-2a)/6]=17+(8-a)/3
2*(a+43)/6=17+(8-a)/3
(a+43)/3-(8-a)/3=17
(a+43-8+a)/3=17
2a+35=17*3=51
2a=51-35
2a=16
a=16/2
a=8
t k chắc, tính nhẩm k cầm mt
HP
26 tháng 3 2016
Ta có:
a+3c=8 (1)
a+2b=9 (2)
Cộng từng vế các BĐT (1);(2)
=>a+3c+a+2b=8+9
=>(a+a)+3c+2b=17
=>2a+2c+c+2b=17
=>2a+2c+2b+c=17
=>2(a+b+c)+c=17
a+b+c lớn nhất <=>c nhỏ nhất
Mà c >= 0 (do c không âm)
=>c=0
Thay c=0 vào (1) ta có:a+3.0=8=>a+0=8=>a=8
Vậy a=8 thỏa mãn
(*)Linh ak,c từng nói t là super làm dài,bài này thì c cũng đâu khác t đâu? 
15 tháng 3 2016
x+3y\(\ge\)1=>x\(\ge\)1-3y
Suy ra: A\(\ge\)(1-3y)2+y2=1-6y+9y2+y2=10y2-6y+1=\(10.\left(y^2-\frac{3}{5}y+\frac{1}{10}\right)\)
\(=10.\left(y^2-2.y.\frac{3}{10}+\frac{9}{100}+\frac{1}{100}\right)=10.\left(x-\frac{3}{10}\right)^2+\frac{1}{10}\ge\frac{1}{10}=0,1\)
Vậy GTNN của A là 0,1 tại x=0,3
sinx=1 =>x=90
=>cos x=cos 90=0
Cách khác: sin x=1 =>sin2x=1
Mà sin2x+cos2x=1 =>1+cos2x=1 =>cos2x=0=>cos x=0