K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

7 tháng 9 2023
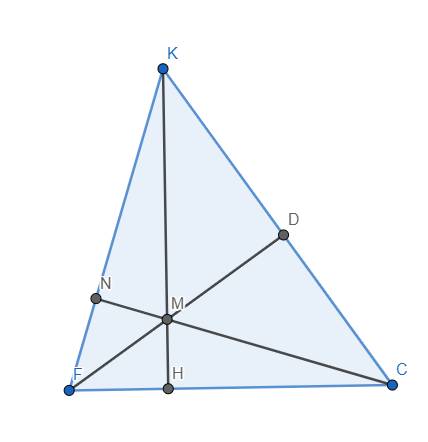
Dễ thấy \(\widehat{HKF}=\widehat{HCM}\) (cùng phụ với \(\widehat{ABC}\))
Xét tam giác HKF và HCM, có: \(\widehat{KHF}=\widehat{CHM}\left(=90^o\right)\) và \(\widehat{HKF}=\widehat{HCM}\) (cmt)
Suy ra \(\Delta HKF~\Delta HCM\left(g.g\right)\)
\(\Rightarrow\dfrac{HK}{HC}=\dfrac{HF}{HM}\) \(\Rightarrow HK.HM=HC.HF\)
Mà \(HC.HF\le\dfrac{\left(HC+HF\right)^2}{4}=\dfrac{FC^2}{4}\) (BĐT Cô-si), suy ra \(HK.HM\le\dfrac{FC^2}{4}\) (đpcm)
Dấu "=" xảy ra \(\Leftrightarrow HC=HF\) \(\Leftrightarrow\) H là trung điểm CF \(\Leftrightarrow\Delta KFC\) cân tại K.
a, Áp dụng ht về lượng trong tam giác vuông FKM,FCM có:
\(FM^2=FH.FK\)
\(FM^2=FT.FC\)
=> FH.FK=FT.FC
b,Có FH.FK=FT.FC <=> \(\frac{FH}{FK}=\frac{FT.FC}{FK^2}\)
Có \(\left\{{}\begin{matrix}FM^2=FH.FK\\FM^2=FT.FC\end{matrix}\right.\) (c/m câu a)<=> \(\left\{{}\begin{matrix}FH=\frac{FM^2}{FK}\\FT=\frac{FM^2}{FC}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\frac{FH}{FK}=\frac{FM^2}{FK^2}\\\frac{FT}{FC}=\frac{FM^2}{FC^2}\end{matrix}\right.\)
Áp dụng ht giữa cạnh và góc trong tam giác vuông FMC,FMK có:
\(sin^2C=\frac{FM^2}{FC^2}=\frac{FT}{FC}\)
\(sin^2K=\frac{FM^2}{FK^2}=\frac{FH}{FK}\)
=> \(sin^2C.sin^2K=\frac{FT}{FC}.\frac{FH}{FK}=\frac{FT}{FC}.\frac{FT.FC}{FK^2}\)( Vì \(\frac{FH}{FK}=\frac{FT.FC}{FK^2}\))=\(\frac{FT^2}{FK^2}\) (1)
Có : FH.FK=FT.FC
<=> \(\frac{FH}{FC}=\frac{FT}{FK}\)
Xét tam giác FHT và FCK có:
\(\frac{FH}{FC}=\frac{FT}{FK}\)
Góc F chung
nên \(\Delta FHT\sim\Delta FCK\)(c-g-c)
=> \(\frac{S_{FHT}}{S_{FKC}}=\left(\frac{FT}{FK}\right)^2\) (2)
Từ (1),(2) => \(\frac{S_{FHT}}{S_{FCK}}=sin^2C.sin^2K\)
P/s :Xem lại đề câu c
Lê Thị Thục HiềnTrần Thanh PhươngVũ Minh Tuấn?Amanda?Nguyễn Việt LâmHISINOMA KINIMADOtthlê thị hương giangsvtkvtm