

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



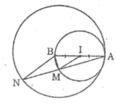
Tam giác AMB nội tiếp trong đường tròn (I) có AB là đường kính nên ![]()
Suy ra: AM ⊥ BM hay BM ⊥ AN
Suy ra: AM = MN (đường kính vuông góc dây cung).

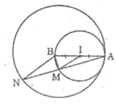
Vì A, I, B thẳng hàng nên:
BI = AB – AI
Vậy đường tròn (I; IA) tiếp xúc với đường tròn (B; BA) tại A.

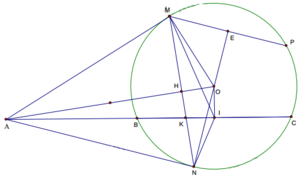
Ta có AN ⊥ NO, MP ⊥ NO, M ∉ AN => AN // MP
Do đó AMPN là hình bình hành ó AN = MP = 2x
Tam giác ∆ANO đồng dạng với ∆NEM => A N N E = N O E M = > N E = 2 x 2 R
TH 1.NE = NO – OE => 2 x 2 R = R − R 2 − x 2 ⇔ 2 x 2 = R 2 − R R 2 − x 2
Đặt R 2 − x 2 = t , t ≥ 0 ⇒ x 2 = R 2 − t 2 .
PTTT 2 ( R 2 − t 2 ) = R 2 − R t ⇔ 2 t 2 − R t − R 2 = 0 ⇔ 2 t = − R t = R
Do t ≥ 0 ⇒ t = R ⇔ R 2 − x 2 = R ⇔ x = 0 ⇒ A ≡ B (loại)
TH 2 NE = NO + OE => 2 x 2 R = R + R 2 − x 2 ⇔ 2 x 2 = R 2 + R R 2 − x 2
Đặt R 2 − x 2 = t , t ≥ 0 ⇒ x 2 = R 2 − t 2 .
PTTT 2 ( R 2 − t 2 ) = R 2 + R t ⇔ 2 t 2 + R t − R 2 = 0 ⇔ 2 t = R t = − R
Do t ≥ 0 ⇒ 2 t = R ⇔ 2 R 2 − x 2 = R ⇔ x = R 3 2 = > A O = 2 R (loại)
Vậy A thuộc BC, cách O một đoạn bằng 2R thì AMPN là hbh

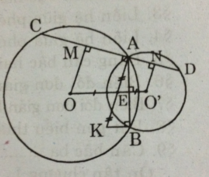
Ta có OO' là đường nối tâm của (O) và (O') nên OO' là đường trung trực của AB.
Suy ra IE ⊥ AB và EA = EB
Ta lại có IA = IK (do K là điểm đối xứng của A qua I).
Nên IE là đường trung bình của tam giác AKB.
Suy ra IE // KB
Mà IE ⊥ AB
Suy ra KB ⊥ AB (đpcm)

a: Xét tứ giác ODAE có
góc ODA+góc OEA=180 độ
=>ODAE là tứ giác nội tiếp
b: \(AE=\sqrt{\left(3R\right)^2-R^2}=2\sqrt{2}\cdot R\)
\(OI=\dfrac{OE^2}{OA}=\dfrac{R^2}{3R}=\dfrac{R}{3}\)
c: Xét ΔDIK vuông tại I và ΔDHE vuông tại H có
góc IDK chung
=>ΔDIK đồng dạng vơi ΔDHE
=>DI/DH=DK/DE
=>DH*DK=DI*DE=2*IE^2