Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) ΔABD cân (AB = AD (gt)) có ∠BAD = 60o nên ΔABD đều
kẻ BJ ⊥ AD ta có:
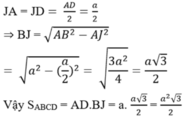

a: Xét tứ giác ABMI có
MI//AB
MI=AB
Do đó; ABMI là hình bình hành
Xét tứ giác AEMF có
góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hìnhchữ nhật
b: \(AB=\sqrt{\dfrac{BC^2}{2}}=\sqrt{32}=4\sqrt{2}\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot4\sqrt{2}\cdot4\sqrt{2}=2\sqrt{2}\cdot4\sqrt{2}=16\left(cm^2\right)\)
c: A đối xứng D qua BC
nên CA=CD
=>CD=AB

A B C D E M 5 cm 4 cm 8 cm
Vì ABCD là hình chữ nhật nên AB = DC = 8 cm ; AD = BC = 4 cm
Ta có: \(MB=AB-AM=8-5=3\left(cm\right)\)
Vì \(AD//BC\) \(\Rightarrow AD//CE\)
Áp dụng hệ quả của định lí Ta-lét: \(\frac{AD}{BE}=\frac{AM}{MB}\Rightarrow BE=\frac{AD.MB}{AM}=\frac{4.3}{5}=2,4\left(cm\right)\)
Suy ra: EC = BE + BC = 2,4 + 4 = 6.4 (cm)
Tam giác ABC vuông tại C:
Áp dụng định lí Pytago ta có: \(DE^2=EC^2+CD^2\Rightarrow DE=\sqrt{EC^2+CD^2}=\sqrt{\left(6,4\right)^2+8^2}=\frac{8\sqrt{41}}{5}\left(cm\right)\)