Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

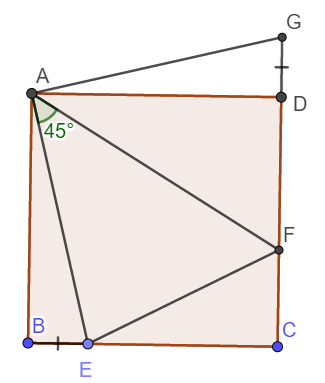
a) Xét tam giác vuông ABE và ADG có:
BE = DG (gt)
AB = AD
\(\Rightarrow\Delta ABE=\Delta ADG\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{BAE}=\widehat{DAG}\) (Hai góc tương ứng)
\(\Rightarrow\widehat{BAE}+\widehat{FAD}=\widehat{DAG}+\widehat{FAD}\)
\(\Rightarrow\widehat{BAE}+\widehat{FAD}=\widehat{FAG}\)
Mà \(\widehat{BAE}+\widehat{FAD}=90^o-\widehat{EAF}=45^o\) nên \(\widehat{FAG}=45^o\)
b) Do \(\Delta ABE=\Delta ADG\Rightarrow AE=AG\)
Xét tam giác AEF và AGF có:
AE = AG (cmt)
Cạnh AF chung
\(\widehat{EAF}=\widehat{GAF}\left(=45^o\right)\)
\(\Rightarrow\Delta AEF=\Delta AGF\left(c-g-c\right)\)
\(\Rightarrow EF=GF=FD+DG=FD+BE\)

A B C E F D
Từ A kẻ đường thẳng Ax vuông góc với AE, trên Ax lấy điểm D sao cho AD=AE. Ta được góc EAD = 90
tgABE=tgACD (c-g-c) do AB=AC( tg ABC vuông cân),góc BAE = góc CAD( cùng phụ với góc EAC),BE=AD(cách vẽ)
=>\(\hept{\begin{cases}BE=DC\\\widehat{B}=\widehat{ACD}\end{cases}}\)
Mà \(\widehat{B}+\widehat{ACF}=90\)nên \(\widehat{ACD}+\widehat{ACF}=90\)=>\(\widehat{DCF}=90\)=>tg DCF là tg vuông
tg EAF = tg FAD(c-g-c) do \(AE=AD,\widehat{EAF}=\widehat{FAD}\left(=45\right),AFchung\)
=> EF=FD
Xét tg vuông FCD vuông tại C có CF2+DC2=FD2( định lý Pytago) <=> CF2+BE2=EF2(do BE=DC,EF=FD)-cmt
đpcm