Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

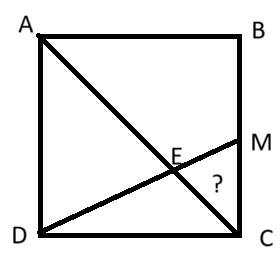
Nối AN và EN
Xét các tam giác AMC và ANC đều = \(\frac{1}{4}\) diện tích hình bình hành = 15 cm2. Mặt khác 2 tam giác này có chung đáy AC \(\Rightarrow\)chiều cao hạ từ đỉnh M xuống đáy AC = chiều cao từ đỉnh N đáy AC.
Xét tam giác ENC và EMC chung đáy EC, chiều cao bằng nhau \(\Rightarrow\)\(S_{ENC}=S_{EMC}\left(1\right)\)
Xét tam giác EDN và ENC chung đỉnh E, đáy DN = NC \(\Rightarrow\)\(S_{EDN}=S_{ENC}\left(2\right)\)
Xét \(S_{AMD}\) = \(S_{AMC}\) có chung AME \(\Rightarrow\)\(S_{AED}=S_{EMC}\left(3\right)\)
Từ (1) ; (2) và (3) \(\Rightarrow\) \(S_{EMC}=S_{ENC}=S_{EDN}=S_{AED}\)
Ta có \(S_{MBC}=\) 15 cm2 \(\Rightarrow\) \(S_{ACD}\)= 15 x 2 = 30 (cm2)
Mà \(S_{ACD}\) \(=S_{ENC}+S_{EDN}+S_{AED}\) và 3 tam giác này bằng nhau nên :
\(S_{ENC}\) = 30 : 3 = 10 (cm2) mà \(S_{ENC}\) = \(S_{MEC}\)
Vậy diện tích MEC = 10 cm2.
\(S_{AMD}=\frac{1}{2}S_{MDC}\)vì đáy \(AM=\frac{1}{2}DC\)và chiều cao kẻ từ \(D\)đến \(AM\)bằng chiều cao kẻ từ \(M\)đến \(DC\)vì cả hai chiều cao đều là chiều cao của hình thang
\(S_{AMD}=\frac{1}{2}S_{MDC}\)mà chung đáy \(MD\)nên chiều cao \(AH=\frac{1}{2}\)chiều cao \(CK\)
Ta có: Chiều cao \(AH\)cũng chính là chiều cao \(\Delta AME\)và chiều cao \(CK\)cũng chính là chiều cao của \(\Delta MEC\)
\(S_{AME}=\frac{1}{2}S_{MEC}\)vì chung đáy \(ME\)và chiều cao \(AH=\frac{1}{2}CK\)
\(\Rightarrow\)Coi \(S_{AME}\)là một phần, \(S_{MEC}\)là hai phần, \(S_{MAC}\)là 3 phần
Ta có: \(S_{MAC}=S_{MBC}\)vì đáy \(MA=MB\)và chung chiều cao kẻ từ \(C\)đến \(AB\)
\(S_{MEC}=15:\left(1+2\right).2=10\left(cm^2\right)\)
Vậy \(S_{MEC}=10cm^2\)

Giải thích các bước giải:
a) Xét tam giác ABC và AMC có chung chiều cao hạ từ đỉnh C mà M là trung điểm AB nên AB = 2 x AM => S_ABC = 2 x S_AMC
Xét tam giác AMC với AMD có chung đáy AM, chiều cao hạ từ đỉnh D đáy AM = chiều cao từ đỉnh C đáy AM => S_AMC = S_AMD.
b) Nối AN và EN
Xét các tam giác AMC và ANC đều = 1/4 diện tích hình bình hành = 15 cm2. Mặt khác 2 tam giác này có chung đáy AC => chiều cao hạ từ đỉnh M xuống đáy AC = chiều cao từ đỉnh N đáy AC.
Xét tam giác ENC và EMC chung đáy EC, chiều cao bằng nhau => S_ENC = S_EMC. (1)
Xét tam giác EDN và ENC chung đỉnh E, đáy DN = NC => S_EDN = S_ENC (2)
Xét S tam giác AMD = S_AMC (phần a đã chứng minh) có chung AME => S_AED = S_EMC (3)
Từ (1) ; (2) và (3) => S_EMC = S_ENC = S_EDN = S_AED.
Ta có S_MBC = 15 cm2 => S_ACD = 15 x 2 = 3 (cm2)
Mà S_ACD = S_ENC + S_EDN + S_AED và 3 tam giác này bằng nhau nên :
S_ENC = 30 : 3 = 10 (cm2) mà S_ENC = S_MEC.
Vậy diện tích MEC = 10 cm2.
c) Từ S_MEC = 10 cm2 => S_MEA = 15 - 10 = 5 (cm2)
Xét có chung chiều cao đỉnh M mà S_MEA/S_MCA = 5/15 = 1/3 =>đáy AE = 1/3 AC
(với cách chứng minh tương tự ta có S_NGC = 5 cm2 và GC = 1/3 AC)
Vậy EG = AC - 1/3 AC - 1/3 AC = 1/3AC
Vậy AE = EG = GC

A B C D E M N O
a) Chu vi hình chữ nhật là :
\(\left(10+6\right)\times2=32\left(cm\right)\)
Do hình vuông có chu vi bằng chu vi hình chữ nhật ấy nên chu vi của hình vuông ABCD là 32 cm
Cạnh hình vuông là :
\(32\div4=8\left(cm\right)\)
b) Do M là điểm chính giữa cạnh AB nên \(AM=MB=\frac{AB}{2}=4\left(cm\right)\)
Ta có \(S_{\Delta ADM}=\frac{AD\times AM}{2}=\frac{8\times4}{2}=16\left(cm^2\right)\)
Do N là điểm chính giữa cạnh BC nên \(BN=NC=\frac{BC}{2}=4\left(cm\right)\)
\(S_{\Delta ABN}=\frac{AB\times BN}{2}=\frac{8\times4}{2}=16\left(cm^2\right)\)
Xét \(\Delta ABN\)và \(\Delta AMN\)có chung đường cao hạ từ N xuống cạnh đáy
Mà đáy AM của \(\Delta AMN\) \(=\frac{1}{2}\)đáy AB của \(\Delta ABN\)
\(\Rightarrow S_{\Delta AMN}=\frac{1}{2}S_{\Delta ABN}=\frac{1}{2}\times16=8\left(cm^2\right)\)
Kẻ \(NO\perp AD\)
Xét tứ giác ABNO có \(\widehat{OAB}=\widehat{ABN}=\widehat{NOA}=90^o\)
\(\Rightarrow\) ABNO là hình chữ nhật
\(\Rightarrow NO=AB=8\left(cm\right)\)
\(S_{\Delta AND}=\frac{NO\times AD}{2}=\frac{8\times8}{2}=32\left(cm^2\right)\)
Vậy ...

Câu 5:
a) Số học sinh nữ của trường Tiểu học đó là:
\(40\%\times850=340\left(hs\right)\)
b) Số học sinh nam của trường Tiểu học là:
\(850-340=510\left(hs\right)\)
Tỉ số phần trăm giữ số học sinh nữ và số học sinh nam là:
\(\left(340\times100\%\right):510=66,67\%\)
Đáp số: ...

Bài 221:
Bán kính hình tròn là:
$12,56:2:3,14=2$ (cm)
Diện tích hình tròn là:
$2\times 2\times 3,14=12,56$ (cm2)
Bài 219:
a. Bán kính: $15:2=7,5$ (cm)
Diện tích hình tròn: $7,5\times 7,5\times 3,14=176,625$ (cm2)
b. Bán kính: $0,2:2=0,1$ (m)
Diện tích hình tròn: $0,1\times 0,1\times 3,14=0,0314$ (m2)
c. Bán kính: $\frac{2}{5}:2=0,2$ (dm)
Diện tích hình tròn: $0,2\times 0,2\times 3,14=0,1256$ (dm2)