Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
=> \(\widehat{ABC}=\widehat{ACB}\) (tính chất tam giác cân).
b) Ta có: \(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
Mà \(\widehat{ECK}=\widehat{ACB}\) (vì 2 góc đối đỉnh).
=> \(\widehat{ABC}=\widehat{ECK}.\)
Hay \(\widehat{DBH}=\widehat{ECK}.\)
Xét 2 \(\Delta\) vuông \(DBH\) và \(ECK\) có:
\(\widehat{DHB}=\widehat{EKC}=90^0\left(gt\right)\)
\(DB=EC\left(gt\right)\)
\(\widehat{DBH}=\widehat{ECK}\left(cmt\right)\)
=> \(\Delta DBH=\Delta ECK\) (cạnh huyền - góc nhọn).
=> \(DH=EK\) (2 cạnh tương ứng).
c) Xét 2 \(\Delta\) vuông \(DHI\) và \(EKI\) có:
\(\widehat{DHI}=\widehat{EKI}=90^0\)
\(DH=EK\left(cmt\right)\)
\(\widehat{DIH}=\widehat{EIK}\) (vì 2 góc đối đỉnh)
=> \(\Delta DHI=\Delta EKI\) (cạnh góc vuông - góc nhọn kề).
=> \(DI=EI\) (2 cạnh tương ứng).
=> \(I\) là trung điểm của \(DE\left(đpcm\right).\)
Chúc bạn học tốt!
Bài 1:
a) Sai đề rồi bạn, đáng lý ra phải là AB=AF mới đúng
Xét ΔABE vuông tại E(AD⊥BE) và ΔAFE vuông tại E(AD⊥BE,F∈BE) có
AE chung
\(\widehat{BAE}=\widehat{FAE}\)(do AE là tia phân giác của góc A)
Do đó: ΔABE=ΔAFE(cạnh góc vuông, góc nhọn kề)
⇒AB=AF(hai cạnh tương ứng)
b) Xin lỗi bạn, mình chỉ biết làm theo cách lớp 8 thôi nhé
Xét tứ giác HFKD có HF//DK(do HF//BC,D∈BC) và HF=DK(gt)
nên HFKD là hình bình hành(dấu hiệu nhận biết hình bình hành)
⇒HD//KF và HD=KF(hai cạnh đối trong hình bình hành HFKD)
c)
Xét ΔABC có AB<AC(gt)
mà góc đối diện với cạnh AB là góc C
và góc đối diện với cạnh AC là góc B
nên \(\widehat{C}< \widehat{B}\)(định lí về quan hệ giữa cạnh và góc đối diện trong tam giác)
hay \(\widehat{ABC}>\widehat{C}\)(đpcm)

A B C I H K
a)
_ Xét \(\Delta\) AKC và \(\Delta\) AHI có :
+ góc AKC = gócÂHB = 90o
+ A là góc chung
+ AB = AC ( gt )
=> \(\Delta\)AHB = \(\Delta\) AKC ( g.c.g)
=> AH = AK ( đpcm )
b)
_ Xét \(\Delta\) AKI và \(\Delta\) AHI có
+ góc AKI = góc AHI = 900
+ AH = AK ( c/m trên )
+ AI là cạnh chung
=> \(\Delta\) AKI = \(\Delta\) AHI ( cạnh huyền - cạnh góc vuông )
=> góc KAI = gócHAI ( 2 góc tương ứng )
c)
_ Xét \(\Delta\) ABD và \(\Delta\) ACD có :
+ AB = AC ( gt )
+ AD chung
+ góc ADB = góc ACD = 90o
=> \(\Delta\)ABD = \(\Delta\) ACD ( cạnh huyền - cạnh góc vuông )
=> AI \(\perp\) BC
Còn lại k biết lm

Đêm qua em hỏi, chị lại ko nghĩ là em :V
Bài 1:
A D C B M N 1 1 1 2
*Hình ảnh chỉ mang tính chất minh họa
a) Ta có: \(xy\)\(//BD\)
Mà \(BD\)là phân giác \(\widehat{ABC}\) \(\Rightarrow BD\)cắt \(BC\)
\(\Rightarrow xy\)cắt \(BC\) ( gọi giao điểm là M )
b) Ta có: \(\widehat{A_1}=\widehat{B_1}\left(slt\right)\) mà \(\widehat{B_1}=\widehat{B_2}\left(gt\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{B_2}\left(1\right)\)
Mặt khác \(\widehat{M_1}=\widehat{B_2}\left(đvi\right)\left(2\right)\)
Từ \(\left(1\right)\&\left(2\right)\Rightarrow\widehat{A_1}=\widehat{M_1}\)
c) Xét \(\Delta BAM\)có \(\widehat{A_1}=\widehat{M_1}\)(câu b)
\(\Rightarrow\Delta BAM\)cân tại \(B\)
\(\Delta BAM\)cân tại \(B\) có \(BN\) là đường phân giác
=> \(BN\)đồng thời là đường cao của \(\Delta BAM\)
=> Đpcm
Bài 2:
x y B 150 K H I
*Hình ảnh chỉ mang tính chất minh họa (Nhinf cais anhr thaays gowms quas)
a) Ta cos: \(AH\) vuông góc \(By\)\(;\) \(CK\)vuông góc \(Bx\)
Mà Bx tạo với tia By một góc 150 độ => Bx cắt By tại B
=> AH cắt CK ( tại giao điểm I )
b) Ta có: \(\widehat{ABC}=150^o\Rightarrow\widehat{ABH}=30^o\)
\(\Rightarrow\widehat{BAH}=90-\widehat{ABH}=60^o\)
\(\Rightarrow\widehat{AIC}=\widehat{AIK}=90-\widehat{BAH}=30^o\)
@@ Cách khác
Ta có: \(\widehat{HBK}=\widehat{ABC}=150^o\left(đđ\right)\)
Xét tứ giác BHIK có:
\(\widehat{AIC}=360-\widehat{IHB}-\widehat{IKB}-\widehat{HBK}\) (Nếu chưa học cái này thì chứng minh bằng cách chia tứ giác thành 2 tam giác)
\(\Leftrightarrow\widehat{AIC}=360-90-90-150=30^o\)
B1 :a)BC ko song song với BD vì chung B
->BC ko sog sog xy (xy//BD) nên cắt BC tại M
b)
c)NBA+ANB+BNA=180^o
NMB+MBN+BNM=180^o
AMB=MAB; B1=B2 (BN pg ABM)
Nen N1=N2;N1+N2=180^o ->ĐPCM
mỏi quá r` mai nghĩ tiếp mà vẽ hộ tui cái hình bài 2 vs

Ta có:3 cạnh hình tam giác có tổng số đo bằng 180 độ
HBM +KMC=90 độ và HBM=KMC
KMH=90 độ
Mik đang học nên gợi ý tính KMH cho bạn và trả lời câu trên thôi
Chúc bạn học tốt!
ta có 3 cạnh tam giác bằng 180o
MBH+CMK=90o và MBH=CMK
HMK=90o

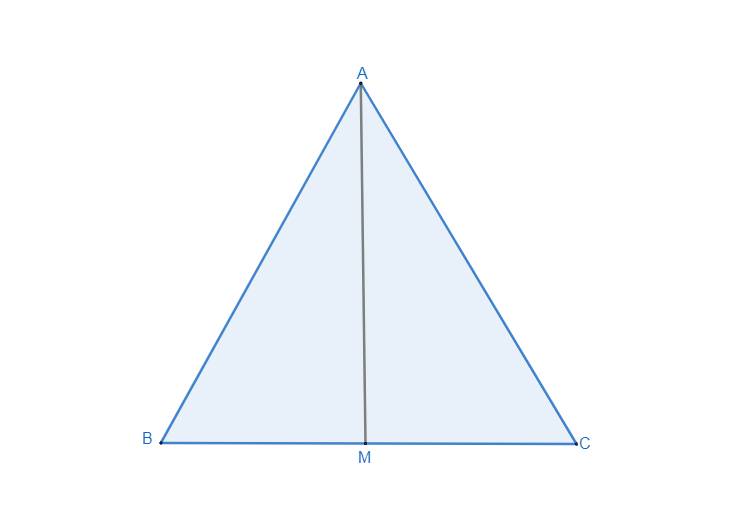

AB = AC (gt)
AM là cạnh chung
MB = MC (do M là trung điểm của BC)
⇒ ∆AMB = ∆AMC (c-c-c)
b) Do ∆AMB = ∆AMC (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∆AMB = ∆AMC (cmt)
⇒ ∠ABM = ∠ACM (hai góc tương ứng)
⇒ ∠ABM = ∠HCM (1)
Do MH // AB (gt)
⇒ ∠ABM = ∠HMC (đồng vị) (2)
Từ (1) và (2) ⇒ ∠HMC = ∠HCM
Do ∆AMB = ∆AMC (cmt)
⇒ ∠MAB = ∠MAC (hai góc tương ứng)
⇒ ∠MAB = ∠HAM (3)
Do MH // AB (gt)
⇒ ∠MAB = ∠HMA (so le trong) (4)
Từ (3) và (4) ⇒ ∠HMA = ∠HAM