Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F K
a) +)EK là đường trung bình nên EK = 1/2 . CD do đó EK < CD
+) EF và AB thì đang suy nghĩ
b) Ta có: \(EK=\frac{1}{2}CD=\frac{CD}{2}\)(t/c đường trung bình)
Tương tự, ta có \(KF=\frac{1}{2}AB\)
Cộng theo vế hai đẳng thức trên ta được:
\(\frac{AB+CD}{2}=EK+KF\ge EF\) ( theo quy tắc 3 điểm)
Đẳng thức xảy ra khi K thuộc EF, khi đó \(\hept{\begin{cases}EK\text{// }CD\\KF\text{//}AB\end{cases}}\) và K thuộc EF nên suy ra \(\hept{\begin{cases}EF\text{//}CD\\EF\text{//}AB\end{cases}}\Leftrightarrow AB\text{//}CD\)
P/s: Chỗ "đẳng thức xảy ra..." mình không chắc.

b) Ta có: \(\frac{AE}{FE}=\frac{DE}{BE}\)(theo cau a)).
\(\Rightarrow\frac{AE}{FE+AE}=\frac{DE}{BE+DE}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AE}{AF}=\frac{DE}{BD}\)(4).
Lại có: \(\frac{KE}{AE}=\frac{DE}{BE}\)(theo câu a)).
\(\Rightarrow\frac{AE}{KE}=\frac{BE}{DE}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AE}{KE+AE}=\frac{BE}{DE+BE}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AE}{AK}=\frac{BE}{BD}\)(5).
Từ (4) và (5).
\(\Rightarrow\frac{AE}{AF}+\frac{AE}{AK}=\frac{DE}{BD}+\frac{BE}{BD}\).
\(\Rightarrow AE\left(\frac{1}{AF}+\frac{1}{AK}\right)=\frac{DE+BE}{BD}\).
\(\Rightarrow AE\left(\frac{1}{AF}+\frac{1}{AK}\right)=\frac{BD}{BD}\).
\(\Rightarrow AE\left(\frac{1}{AF}+\frac{1}{AK}\right)=1\).
\(\Rightarrow\frac{1}{AF}+\frac{1}{AK}=\frac{1}{AE}\)(điều phải chứng minh).

Hình bạn tự vẽ nhá !!
Xét \(\Delta BEC\) và \(\Delta CDB\) có :
\(\widehat{EBC}=\widehat{DCB}\left(gt\right)\); \(BC\)chung; \(\widehat{DBC}=\widehat{ECB}\left(=\frac{1}{2}\widehat{ABC}=\frac{1}{2}\widehat{ACB}\right)\)
\(\Rightarrow\Delta BEC=\Delta CDB\) \(\left(g-c-g\right)\)\(\Rightarrow BE=CD\)
Do đó \(\frac{BE}{AB}=\frac{CD}{AC}\) theo định lý Ta lét đảo \(\Rightarrow DE//BC\)
\(\Rightarrow\widehat{DBC}=\widehat{EDB}=\widehat{EBD}\) (SLT)
\(\Rightarrow\Delta BED\) cân tại \(E\) \(\Rightarrow DE=BE=c\)
Do DE//BC ta có : \(\frac{DE}{BC}=\frac{AE}{AB}\) (ĐL Talét) (1) Và \(\frac{DE}{AB}=\frac{BE}{AB}\) (2)
Cộng vế với vế của (1) và (2) ta được : \(\frac{DE}{BC}+\frac{DE}{AB}=\frac{AE}{AB}+\frac{BE}{AB}=\frac{AE+BE}{AB}=\frac{AB}{AB}=1\)
\(\Leftrightarrow DE\left(\frac{1}{AB}+\frac{1}{BC}\right)=1\Rightarrow\frac{1}{AB}+\frac{1}{BC}=\frac{1}{DE}\)
Hay \(\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\) (ĐPCM)
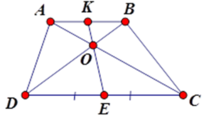
Theo định lý Ta-lét:
Vì AK // EC nên A K E C = O K O E và KB // ED nên B K E D = O K O E = O B O D từ đó A K E C = K B D E và A K E C = O B O D
Mà EC = ED => AK = KB
Nên (I), (II), (IV) đúng
Vì AB // DC => A O O C = A B D C nên (III) sai
Đáp án: C