Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

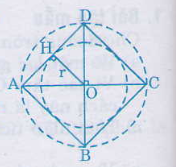
a) Chọn điểm O làm tâm , mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm: (O; 2cm)
Vẽ bằng eke và thước thẳng.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O;2cm)
c) Vẽ OH ⊥ AD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
r = OH = AH.
r2 + r2 = OA2 = 22 => 2r2 = 4 => r = √2 (cm)
Vẽ đường tròn (O;√2cm). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh

a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
Hướng dẫn trả lời:
a) Dùng êke ta vẽ hình vuông ABCD có cạnh bằng 4cm như sau:
- Vẽ AB = 4cm.
- Vẽ BC ⊥ AB và BC = 4cm
- Vẽ DC ⊥ BC và DC = 4cm
- Nối D với A, ta có AD ⊥ DC và AD = 4cm
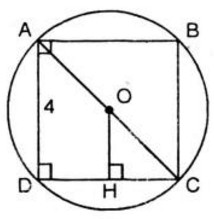
b) Tam giác ABC là tam giác vuông cân nên AB = BC.
Áp dụng định lí Py – ta – go trong tam giác vuông ABC, ta có:
AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=√32=4√2AC2=AB2+BC2=2AB2⇔AC2=2.42=32⇒AC=32=42
Vậy AO=R=AC2=4√22=2√2AO=R=AC2=422=22
Vậy R = 2√2 cm
c) Vẽ OH ⊥ Dc. Vẽ đường tròn tâm O, bán kính OH. Đó là đường tròn nội tiếp hình vuông ABCD
Ta có: OH=AD2=2(cm)OH=AD2=2(cm)
Vậy r = OH = 2cm
\

Bạn ra đề như hình vẽ mà, tụi mình đâu có biết hình như thế nào mà vẽ đây!![]()

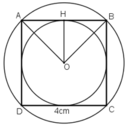
a) Vẽ hình vuông ABCD có cạnh 4cm.
b) Vẽ hai đường chéo AC và BD. Chúng cắt nhau tại O.
Đường tròn (O; OA) là đường tròn ngoại tiếp hình vuông ABCD.
Ta có:
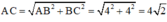 (cm)
(cm)
⇒ R = OA = AC/2 = 2√2 (cm).
c) Gọi H là trung điểm AB.
(O ; OH) là đường tròn nội tiếp hình vuông ABCD.
r = OH = AD/2 = 2cm.