Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y tỉ lệ nghịch với x
=>x1.y1=x2.y2
=>5y1=6y2
=>y1=6/5.y2
mà 7y1-8y2=3(-1)=1/3
=>7.6/5.y2-8y2=1/3
=>2/5y2=1/3
=>y2=5/6
vì y TLN với x
=>hệ số tỉ lệ a=x2.y2=6.5/6=5
=>x.y=5
y=-5
=>x=-1
(lâu ko làm dạng này nên ko chắc nhé ^^)

a: Ta có: \(\hat{AOD}+\hat{BOD}=180^0\) (hai góc kề bù)
=>\(\hat{BOD}=180^0-97^0=83^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\hat{AOE}<\hat{AOD}\left(56^0<97^0\right)\)
nên tia OE nằm giữa hai tia OA và OD
=>\(\hat{AOE}+\hat{EOD}=\hat{AOD}\)
=>\(\hat{EOD}=97^0-56^0=41^0\)
Ta có: \(\hat{AOE}+\hat{EOC}+\hat{COB}=180^0\)
=>\(\hat{EOC}=180^0-56^0-42^0=82^0\)
b: Trên cùng một nửa mặt phẳng bờ chứa tia OE, ta có; \(\hat{EOD}<\hat{EOC}\left(41^0<82^0\right)\)
nên tia OD nằm giữa hai tia OE và OC
=>\(\hat{EOD}+\hat{DOC}=\hat{EOC}\)
=>\(\hat{DOC}=82^0-41^0=41^0\)
Ta có: tia OD nằm giữa hai tia OE và OC
\(\hat{DOE}=\hat{DOC}\left(=41^0\right)\)
Do đó: OD là phân giác của góc EOC

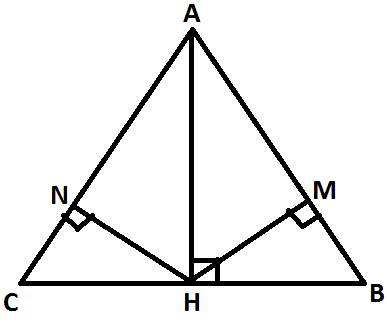

Ta có \(MN\perp AC\Rightarrow\) Tam giác AHC vuông tại H ; Tam giác AHB vuông tại H
Do \(\widehat{A_1}=\widehat{A_2}\) , \(\widehat{AHC}=\widehat{AHB}\left(=90^o\right)\)
Suy ra được 2 góc còn lại của 2 tam giác bằng nhau
\(a,\) Xét \(\Delta AHC\) và \(\Delta AHB:\)
Có 3 góc trong tam giác đều bằng nhau \(\Rightarrow\Delta AHC=\Delta AHB\left(g-g-g\right)\)
\(b,\) \(\widehat{A_1}=\widehat{A_2}\Rightarrow\) A là đường phân giác của tam giác ABC\(\Rightarrow HC=HB\)
Xét \(\Delta HNC\) và \(\Delta HMB:\)
Có 2 góc bằng nhau \(\widehat{M}=\widehat{N}\left(=90^o\right);\widehat{C}=\widehat{B}\left(cmt\right)\)
Và \(HC=HB\left(cmt\right)\)
\(\Rightarrow\Delta HNC=\Delta HMB\left(g-c-g\right)\)
`MN` ở đâu vậy ạ?