Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AB → = (−1; −2; 1)
AC → = (−1; −3; 0)
Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto AB → và AC → cùng phương, nghĩa là AB → = k AC → với k là một số thực.
Giả sử ta có AB → = k AC →
khi đó 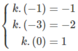
Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên. Vậy ba điểm A, B, C không thẳng hàng.
Cho hai bộ ba điểm: M = (1; 1; 1), N = (-4; 3; 1), P = (-9; 5; 1). Hỏi bộ nào có ba điểm thẳng hàng?

Ta có: MN → = (−5; 2; 0) và MP → = (−10; 4; 0). Hai vecto MN → và MP → thỏa mãn điều kiện: MN → = k MP → với k = k/2 nên ba điểm M, N, P thẳng hàng.

Gọi Q là mặt phẳng đi qua A và song song với (P) thì phương trình của (Q) là \(\left(x+2\right)+2\left(y+1\right)-\left(z-1\right)=0\) hay \(x+2y-z+5=0\). Gọi H là hình chiếu vuông góc của B lên (Q). Giả sử \(\Delta\) là đường thẳng qua A và song song với


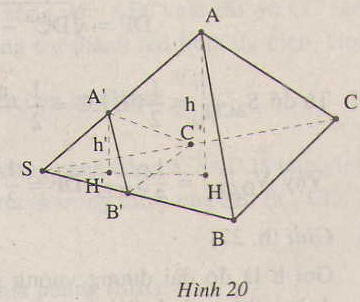
Gọi h và h’ lần lượt là chiều cao hạ từ A, A’ đến mặt phẳng (SBC).
Gọi S1 và S2 theo thứ tự là diện tích các tam giác SBC và SB’C’.
Khi đó ta có h′h=SA′SAh′h=SA′SA và 12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC
Suy ra VS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SCVS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SC
Đó là điều phải chứng minh.

Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :

Bài 1: Thực hiện phép tính
a)136 - (2 . 52 + 23 . 3)
= 136 - (104 + 69)
= 136 - 173
= -37
b) (-243) + (-12) + (+243) + (-38) + (10)
= [(-243) + (+243)] + (-12) + (-38) + (10)
= 0 + (-40)
= -40
Bài 2 : Tìm x ∈ N, biết:
a) 6 . (x-81) = 54
⇒ x - 81 = 54 : 6
⇒ x - 81 = 9
x = 81 + 9
x = 90
Vậy : x = 90
b) 18 - (x-4) = 32
⇒ x - 4 = 18 - 32
⇒ x - 4 = -14
x = -14 + 4
x = -10

Theo định nghĩa ta thấy kết quả:
a) HÌnh trụ tròn xoay có đường cao là cạnh thứ tư còn bán kính hình trụ bằng độ dài của cạnh kề với cạnh thứ tư đó.
b) Hình nón tròn xoay có chiều cao bằng chiều cao của tam giác cân, cond bán kính đáy bằng một nửađộ dài cạnh đáy của tam giác cân đó.
c) Khối nón tròn xoay.
d) Khối trụ tròn xoay.

Gọi độ dài của ba đoạn thẳng đã cho là a. Khi đó các đầu mút của chúng là đỉnh của một hình tám mặt đều, mỗi mặt là tam giác đều có cạnh bằng \(\dfrac{a\sqrt{2}}{2}\)

