Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
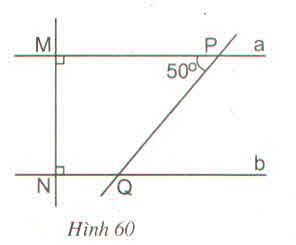
a) Hai đường thẳng a và b cùng vuông góc với đường thẳng MN nên a // b.
b) Ta có góc MPQ = góc Q1 = 50o (so le trong vì a // b)
mà góc Q1 + Q2 = 180o (kề bù)
=> Q2 = 180o - 50o = 130o
Vậy góc NQP = 130o.
Kí hiệu như hình vẽ.
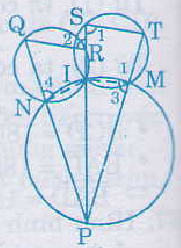
Ta có tứ giác ISTM nội tiếp đường tròn nên:
ˆS1S1^ + ˆMM^ = 180o
Mà ˆM1M1^ + ˆM3M3^ = 180o (kề bù)
nên suy ra ˆS1S1^ = ˆM3M3^ (1)
Tương tự từ các tứ giác nội tiếp IMPN và INQS ta được
ˆM3M3^ = ˆN4N4^ (2)
ˆN4N4^ = ˆR2R2^ (3)
Từ (1), (2), (3) suy ra
Do đó QR // ST
help me
Theo mình nghĩ thì đề thiếu là tam giác ABC vuông tại A nhé!
Bạn xem lại đề!:)
. Chứng minh A > 
– | x – 2|
\(VT=\dfrac{a+c}{a+b}+\dfrac{b+d}{b+c}+\dfrac{c+a}{c+d}+\dfrac{d+b}{d+a}\)
\(=\left(a+c\right)\left(\dfrac{1}{a+b}+\dfrac{1}{c+d}\right)+\left(b+d\right)\left(\dfrac{1}{b+c}+\dfrac{1}{d+a}\right)\)
Ap dụng \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y} \left(\forall x,y>0\right)\)
Ta có: \(VT\ge\left(a+c\right).\dfrac{4}{a+b+c+d}+\left(b+d\right).\dfrac{4}{a+b+c+d}\)
\(=\dfrac{4\left(a+b+c+d\right)}{\left(a+b+c+d\right)}=4\left(ĐPCM\right)\)
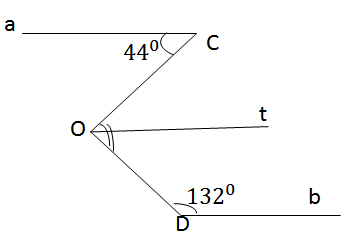
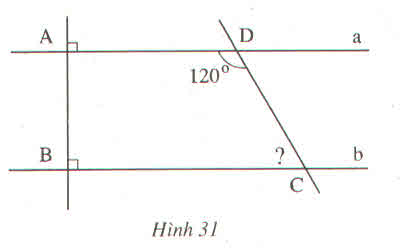
a, Ta có:
AB \(\perp\) a
AB \(\perp\) b
\(\Rightarrow\)a // b
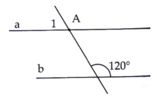
b, Ta có: a // b( câu a)
hai góc ADC và DCB là hai góc trong cùng phía
\(\Rightarrow\)DCB = 180\(^0\) - ADC(tính chất hai đường thẳng song song)
\(\Rightarrow\) DCB = 180\(^0\)-120\(^0\) = 60\(^0\)
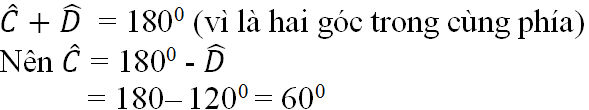
Chọn A