PT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
29 tháng 11 2023
a/
\(Ax\perp m\left(gt\right);By\perp m\left(gt\right)\) => Ax//By (cùng vuông góc với m)
Mà Cz//Ax (gt)
=> Cz//By (cùng // với Ax)
b/
\(\widehat{BCz}=\widehat{ACB}-\widehat{C}=110^o-30^o=80^o\)
Ta có
Cz//By (cmt) \(\Rightarrow\widehat{BCz}=\widehat{CBy}=80^o\) (góc so le trong)
c/
\(CD\perp Ax\left(gt\right)\Rightarrow\widehat{ADC}=90^o\)
Cz//Ax (gt) \(\Rightarrow\widehat{A}=\widehat{C}=30^o\) (Góc so le trong)
Xét tg vuông ACD có
\(\widehat{ACD}=\widehat{ADC}-\widehat{A}=90^o-30^o=60^o\)
AD
9 tháng 2 2021
a) Có : AB=AC(tg ABC cân tại A)
BD=CE(gt)
=> AB+BD=AC+CE
=> AD=AE
=> Tg ADE cân tại A
\(\Rightarrow\widehat{D}=\widehat{E}=\frac{180^o-\widehat{A}}{2}\)
Lại có : \(\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{A}}{2}\)(tg ABC cân tại A)
\(\Rightarrow\widehat{D}=\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\)
Mà chúng là 2 góc đồng vị
=> BC//DE
b) Có : \(\widehat{CBD}=180^o-\widehat{ABC}\)
\(\widehat{BCE}=180^o-\widehat{ACB}\)
Mà : \(\widehat{ABC}=\widehat{ACB}\)(tg ABC cân tại A)
\(\Rightarrow\widehat{CBD}=\widehat{BCE}\)
- Xét tg BCD và CBE có :
BD=CE(gt)
BC-cạnh chung
\(\widehat{CBD}=\widehat{BCE}\left(cmt\right)\)
=> Tg BCD=CBE(c.g.c)
=> BE=CD(đccm)
c) Có : \(\widehat{KBC}=\widehat{KCB}\)(tg BCD=CBE)
=> Tg KBC cân tại K
- Có : \(\widehat{KDE}=\widehat{ADE}-\widehat{ADC}\)
\(\widehat{KED}=\widehat{AED}-\widehat{AEB}\)
Mà : \(\widehat{AED}=\widehat{ADE}\)(tg ADE cân tại A)
\(\widehat{ADC}=\widehat{AEB}\)(tg BCD=CBE)
\(\Rightarrow\widehat{KED}=\widehat{KDE}\)
=> Tg KDE cân tại K
d) Xét tam giác ABK và ACK có :
AB=AC(tg ABC cân tại A)
AK-cạnh chung
KB=KC(tg KBC cân tại K)
=> Tg ABK=ACK(c.c.c)
=> \(\widehat{BAK}=\widehat{CAK}\)
=> AK là tia pg góc BAC
e) Không thấy rõ đề : DM và EN như thế nào so với BC?
16 tháng 8 2017
Gọi By' là tia đối của tia By.
Gọi I là giao điểm của AC và yy'
By//Ax (gt) nên By'//Ax
Do By'//Ax nên xAC=AIy' ( so le trong)
Ta lại có: AIy=BIC ( đối đỉnh)
Do yBC là góc ngoài tại đỉnh B của tam giác BCI nên:
yBC=BIC+ACB
Mà xAC=AIy'
BIC=AIy'
=> xAC=BIC
Do đó yBC=xAC+ACB (đpcm)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
25 tháng 12 2021
a/ Xét \(\Delta ABD\) và \(\Delta KBD\)
AB=BK (gt); BD chung
\(\widehat{ABD}=\widehat{KBD}\) (gt)
\(\Rightarrow\Delta ABD=\Delta KBD\left(c.g.c\right)\Rightarrow AD=DK\)
b/
\(\Delta ABD=\Delta KBD\Rightarrow\widehat{BAC}=\widehat{BKD}=90^o\Rightarrow DK\perp BC\)
\(AH\perp BC\left(gt\right)\)
=> AH//DK (cùng vuông góc với BC)
c/
Gọi M' là giao của BD với CE. Xét \(\Delta BCE\) có
\(EK\perp BC,CA\perp BE\)=> D là trực tâm của \(\Delta BCE\Rightarrow BM\perp CE\) (trong tam giác 3 đường cao đồng quy tại 1 điểm gọi là trực tâm của tam giác)
Mà BM là phân giác của \(\widehat{ABC}\Rightarrow\Delta BCE\) cân tại B (trong tam giác đường cao đồng thời là đường phân giác thì tg đó là tg cân)
=> BM' là đường trung tuyến (trong tg cân đường cao xp từ đỉnh đồng thời là đường trung tuyến của tam giác)
=> M' là trung điểm của CE, mà M cũng là trung điểm của CE => M trùng M' => B, D, M thẳng hàng
18 tháng 10 2016
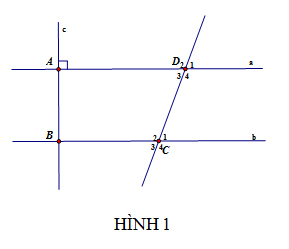
trc hết D1= 70O
a) D1 = D3= 70 (đối đỉnh)
C2 + D3 = 110+70 = 180 ( 2 góc này ở
vị trí trong cùng phía) nên a//b
b) theo a) có a//b
mà c vuông góc với a => c vuong goc voi b
CP
4 tháng 6 2020
a) △ABC có : Hai đường cao BE và AD mà 2 đường này cùng cắt nhau tại điểm I ⇒ I là trực tâm
⇒ CI là đường cao còn lại ⇒ CI ⊥ AB
b) Xét △BEC có : góc EBC + gócBEC + góc BCE = \(180^0\)( định lí tổng ba góc )
⇒ góc EBC = \(180^0\) - góc BEC - góc BCE = \(180^0\)- \(90^0\)-\(40^0\)= \(50^0\)
Lại xét △BID có : góc BID + góc IBD + góc BDI = \(180^0\)
⇒ góc BID = \(180^0\) - \(90^0\) - \(50^0\) = \(40^0\)
Có góc BID + góc DIE = \(180^0\)( 2 góc kề bù )
⇒ góc DIE = \(180^0\) - góc BID = \(180^0-40^0\)= \(140^0\)
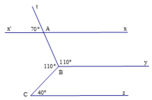
a) Ta có x'At ^ + tAx ^ = 180 ∘ (hai góc kề bù)
mà x'At ^ = 70 ∘
⇒ xAt ^ = 180 ∘ − 70 ∘ = 110 ∘
Mặt khác ABy ^ = 110 ∘
⇒ xAt ^ = ABy ^ mà hai góc này ở vị trí đồng vị
⇒ By // xx'
b)
Kẻ tia By' là tia đối của tia By
Vì By // xx' nên By' // xx'
⇒ x'At ^ = ABy' ^ = 70 ∘ (hai góc đồng vị)
Mặt khác ABC ^ = ABy' ^ + y'BC ^
Mà ABC ^ = 110 ∘ và ABy' ^ = 70 ∘
⇒ y'BC ^ = 110 ∘ − 70 ∘ = 40 ∘
Ta lại có BCz ^ = 40 ∘
⇒ y'BC ^ = BCz ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
ko bit cạch trl