Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam giác BCD có CA vừa là đường cao vừa là trung tuyến
=> tam giác BCD cân tại C
b) Tam giác BCD cân tại C có CA là đường cao
=> CA đồng thời là phân giác
Vậy CA là phân giác góc BCA
=> AH = AK (tính chất tia phân giác)
Chứng minh: (nếu chưa học)
Xét 2 tam giác vuông: tgiac CHA và tgiac CKA có:
cạnh CA: chung
góc HCA = góc KCA (cmt)
suy ra: tgiac CHA = tgiac CKA (ch_gn)
=> AH = AK; CH = CK
c) Tam giác CHK cân tại C (CH = CK)
=> \(\widehat{CHK}=\frac{180^0-\widehat{C}}{2}\) (1)
Tam giác BCD cân tại C
=> \(\widehat{CBD}=\frac{180^0-\widehat{C}}{2}\) (2)
Từ (1) và (2) suy ra: góc CHK = góc CBD
mà 2 góc này đồng vị
=> HK // BD
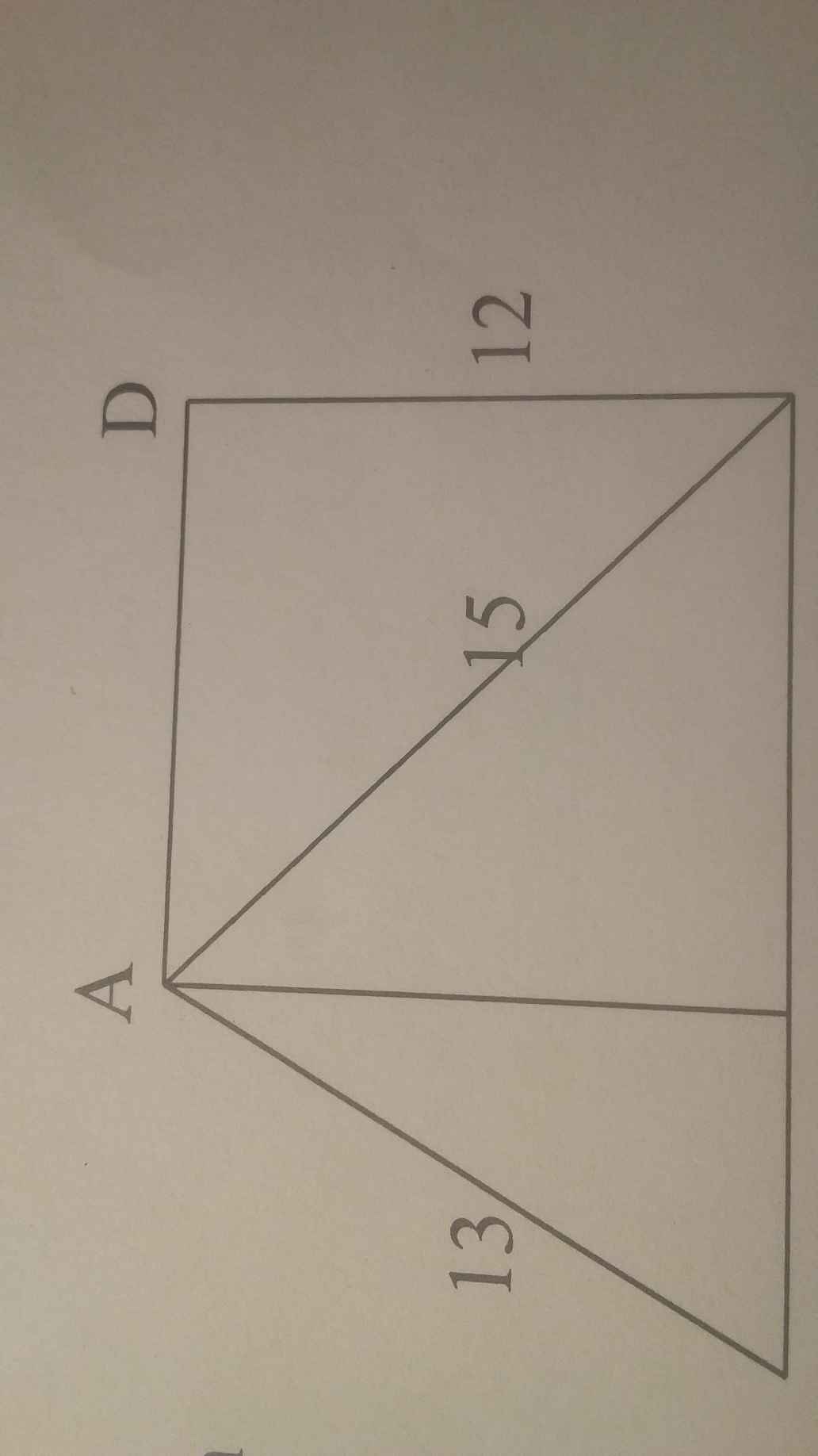
d) Áp dụng Pytago ta có:
AB2 + AC2 = BC2
=> AB2 = BC2 - AC2 = 144
=> AB = 12
=> BD = 2AB = 24

A B C H K E D F
c, có ^DAB = ^FAC = 90
^DAB + ^BAC = ^DAC
^FAC + ^BAC = ^FAB
=> ^DAC = ^FAB
xét tg DAC và tg BAF có : AD = AB (gt) và AF = AC (Gt)
=> tg DAC = tg BAF (C-g-c)
=> BF = DC (đn)

b
AH vuông góc với BC
BC song song với EK
=>AH vuông góc với EK

Xét tứ giác \(ADCH\) có:
\(\widehat{D}=\widehat{C}=\widehat{H}=90^o\)
\(\Rightarrow ADCH\) là hình chữ nhật
\(\Rightarrow AH=DC=12cm\)
Xét \(\Delta ADC\left(\widehat{D}=90^o\right)\) có:
\(AC^2=AD^2+DC^2\) (định lí pitago)
\(\Rightarrow AD=\sqrt{AC^2-DC^2}=\sqrt{15^2-12^2}=9cm=HC\)
Xét \(\Delta ABH\left(\widehat{H}=90^o\right)\) có:
\(AB^2=AH^2+BH^2\) (định lí pitago)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{13^2-12^2}=5cm\)
\(\Rightarrow BC=BH+HC=5+9=14cm\)
Vậy \(BC=14cm\)