Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(B=3+3^2+3^3+...+3^{120}\)
\(B=3\cdot1+3\cdot3+3\cdot3^2+...+3\cdot3^{119}\)
\(B=3\cdot\left(1+3+3^2+...+3^{119}\right)\)
Suy ra B chia hết cho 3 (đpcm)
b) \(B=3+3^2+3^3+...+3^{120}\)
\(B=\left(3+3^2\right)+\left(3^3+3^4\right)+\left(3^5+3^6\right)+...+\left(3^{119}+3^{120}\right)\)
\(B=\left(1\cdot3+3\cdot3\right)+\left(1\cdot3^3+3\cdot3^3\right)+\left(1\cdot3^5+3\cdot3^5\right)+...+\left(1\cdot3^{119}+3\cdot3^{119}\right)\)
\(B=3\cdot\left(1+3\right)+3^3\cdot\left(1+3\right)+3^5\cdot\left(1+3\right)+...+3^{119}\cdot\left(1+3\right)\)
\(B=3\cdot4+3^3\cdot4+3^5\cdot4+...+3^{119}\cdot4\)
\(B=4\cdot\left(3+3^3+3^5+...+3^{119}\right)\)
Suy ra B chia hết cho 4 (đpcm)
c) \(B=3+3^2+3^3+...+3^{120}\)
\(B=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+\left(3^7+3^8+3^9\right)+...+\left(3^{118}+3^{119}+3^{120}\right)\)
\(B=\left(1\cdot3+3\cdot3+3^2\cdot3\right)+\left(1\cdot3^4+3\cdot3^4+3^2\cdot3^4\right)+...+\left(1\cdot3^{118}+3\cdot3^{118}+3^2\cdot3^{118}\right)\)
\(B=3\cdot\left(1+3+9\right)+3^4\cdot\left(1+3+9\right)+3^7\cdot\left(1+3+9\right)+...+3^{118}\cdot\left(1+3+9\right)\)
\(B=3\cdot13+3^4\cdot13+3^7\cdot13+...+3^{118}\cdot13\)
\(B=13\cdot\left(3+3^4+3^7+...+3^{118}\right)\)
Suy ra B chia hết cho 13 (đpcm)

vì góc xOz là góc kề bù=>góc xOz=180 do
=>Tia Oy nằm giữa 2 tia Ox; Oz
Vì tia Oy nằm giữa 2 tia Ox; Oz=>xOy+yOz=xOz
Thay xOy=60do;xOz=180do
60+yOz=180
yOz=180-60
yOz=60

giải
a / do góc xoz = 20 độ
góc yoz =xoy-xoz
= 110-20=90
b/ vid om là phân gics của yoz => zom=yom
=> xom=xoz+zom=20+45=65 độ
c/ đg kính bn cm cậu


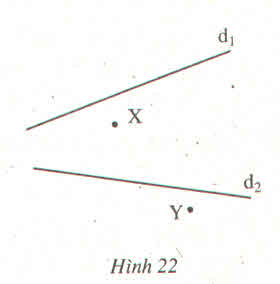
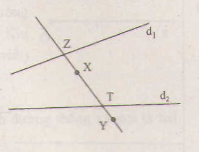
Ba điểm X,Z,T thẳng hàng vậy X nằm trên đường thẳng ZT.
– Ba điểm Y,Z,T thẳng hàng vì vậy Y nằm trên đường thẳng ZT.
Suy ra X,Y nằm trên đường thẳng ZT, dó đó 4 điểm Z,Y,Z,T thẳng hàng.
nối hai điểm X,Y kéo dài lại với nhau X,Ycắt d2 tai z ,X,Y căt d2 tại T

a, lấy BC-BD thì sẽ ra DC thôi
b,lấy góc BAD + DAC
C, THÌ có mỗi ABD và ADC kề nhau và kề bù trong hình vẽ thôi
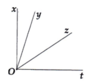

Các cặp góc phụ nhau có trong hình vẽ: x O z ^ v à z O t ^ ; x O y ^ v à y O t ^ .