Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,
góc QPN=góc QMN=80
góc PNM=góc PQM=100
Giải thích các bước giải:
a. Gọi E là giao của AC và BD
ABCD là hình thang cân -> AC=BD
Xét ΔDQP và ΔCNP có
DQ=CN=(AC2AC2 = BD2BD2 )
góc QDP = góc NCP
DP=CP
-> ΔDQP = ΔCNP (c.g.c)
-> góc DPQ=góc CPN
Xét ΔDEP và ΔCEP có
DE=CE
cạnh EP chung
DP=CP
-> ΔDEP = ΔCEP (c.c.c)
-> góc DPE=góc CPE=90
<-> góc DPQ + góc QPE= góc CPN+góc NPE
-> góc QPE = góc NPE
-> PM là tia phân giác của góc QMN
b. Vì Q,P là trung điểm DB,DC
-> QP là đường trung bình -> QP=BC2BC2, QP//BC
CM tương tự MN=BC2BC2
PN=AD2AD2
QM=AD2AD2
Mà AD=BC
-> QP=MN=PN=QM
-> QPNM là hình thoi
Vì QP//BC -> góc DPQ=góc DCB=50
góc QPM=góc DPM-góc DPQ=90-50=40
góc QPN=2.góc QPM=2.40=80
góc PNM=180-góc QPN=100
góc QPN=góc QMN=80
góc PNM=góc PQM=100
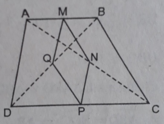
A M B Q N P D C
a.Vì M, N , P, Q là trung điểm AB, AC, DC, DB
=> MN,NP,PQ,QM là đường trung bình ΔABC,ACD,DBC,ABD
\(\Rightarrow MQ=PN=\frac{1}{2}AD,MN=PQ=\frac{1}{2}BC\)
Mà AD = BC => MN = NP = QM => MNPQ là hình thoi
=> PM là tia phân giác ^QPN
b ) Vì PN // AD => \(\widehat{NPC}=\widehat{ADC}=50^0\)
\(\Rightarrow\widehat{MPQ}=\widehat{MPN}=90^0-50^0=40^0\Rightarrow\widehat{NPQ}=80^0\)
Vì ABCD là hình thang cân , M, N là trung điểm AB ,CD
=> \(MP\perp DC,AB\)
Do MNPQ là hình thoi
\(\Rightarrow\widehat{QMN}=\widehat{QPN}=80^0\Rightarrow\widehat{MQP}=\widehat{MNP}=180^0-80^0=100^0\)

a / hình bình hành
b/ AC=BD ; AB>CD ; AB<AC<CD;AB<BD<CD
c/hình vuông
(Hình thì bạn tự vẽ nha)
a) Xét tam giác BAD có: MB=MA ; QB=QD
=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN
=> MNPQ là hình thoi

a/Có AB//CD nên \(\frac{AB}{CD}=\frac{MB}{DP}=\frac{MA}{PC}\).Theo hệ quả Thales thì ta có
AC, BD, MP đồng quy
Ta có M,N,Q là tđ AB,AC,BD nên \(MN=\frac{1}{2}BC,MQ=\frac{1}{2}AD\)
BC=AD nên MN=MQ(1)
Tương tự QP=NP =1/2AD=1/2BC(2)
Từ (1) và (2) suy ra MNPQ là h/thoi \(\Rightarrow\)MP là tia phấn giác QMN
b/
Có : \(\widehat{DAB}=\widehat{CBA}=\widehat{AMN}=\widehat{BMQ}=130\)
Mà \(\widehat{BMN}=\widehat{AMQ}=50\Rightarrow\widehat{QMN}=80\)
Tgiac QMN cân nên tính đc các góc còn lại

MNPQ là hình thoi vì là hình bình hành có hai cạnh kề bằng nhau.