Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Hinh thang ABCD la hinh thang can
AD=BC
goc D=goc C
Xet tam giac AED vuong va tam giac BFC vuong
Ta co: AD=BC( 2 canh ben hinh thang can)
Goc D=goc C( 2 goc ke 1 day )
=> tam giac AED = Tam giac BFC ( canh huyen - goc nhon )
=> DE=CF
a: Xét ΔAED vuông tại E và ΔBFC vuông tai F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
Suy ra: DE=CF
b: Gọi O là giao điểm của AD và BC
Xét ΔODC có AB//CD
nên OA/AD=OB/BC
=>OA=OB
=>ΔOAB cân tại O
=>OI vuông góc với BA(1)
Xét ΔODC có OD=OC
nên ΔODC cân tại O
=>OK vuông góc với CD
=>OK vuông góc với AB(2)
Từ (1) và (2) suy ra O,I,K thẳng hàng(ĐPCM)
c: Xét ΔIAD và ΔIBC có
IA=IB
góc IAD=góc IBC
AD=BC
Do đó: ΔIAD=ΔIBC
Suy ra: ID=IC
Xét ΔMED vuông tại E và ΔNFC vuông tại F có
MD=NC
góc MDE=góc NCF
Do đó: ΔMED=ΔNFC
Suy ra: MD=NC
Xét ΔIDC có IM/ID=IN/IC
nên MN//DC
=>DMNC là hình thang
mà góc MDC=góc NCD
nên DMNC là hìh thang cân

Z bn giải giúp mình vs !!! Bn đủ thông minh để bài toán lớp 5 này mak he .

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E

Xét tam giác ADE và BCF có:
góc E = góc F=90 độ
AD=BC ( ABCD là hình thang cân)
góc D = góc C
=> tam giác ADE = tam giác BCF (ch-gn)
quá dễ luôn
=> AE=BF ( 2 cạnh tương ứng)

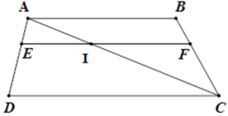
Gọi I là giao điểm của AC và EF.
Xét tam giác ACB có IF // AB nên theo định lý Ta-lét ta có
B F B C = A I A C = A E A D = 4 12 = 1 3 nên BF = 1 3 .BC = 1 3 .15 = 5 (cm)
Đáp án: B

A B C D E F
Xét 2 tam giác vuông \(\Delta AED\)Và \(\Delta BFC\) CÓ :
\(\widehat{ADE}=\widehat{BCF}\)( Hình thang cân nên 2 góc kề đáy bằng nhau)
\(AD=BC\)( hình tháng cân có 2 cạnh bên bằng nhau )
=> 2 tam giác bằng nhau ( cạnh huyền - góc nhọn )
=> \(DE=CF\)( 2 cạnh tương ứng )
a) Ta có: AE//BF vì cung vuông góc CD
AB//CD// EF (E,F thuộc CD)
=> ABFE là hình bình hành
=> AE=EF
b) Gọi I là tđ AB, K là tđ CD
=> IK vuông góc AB,CD vì ABCD là hình thang cân
Vì đường chéo hình thang cân cắt nhau tại 1 điểm chắc chắn thuộc IK( Tính chất hình thang cân)
=> KI//AE//BF
Mà CF = DE
=> K cũng là trung điểm CD
=> MJ//AE//BE
Đúng thì tim giúp nha bạn. Thx