Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABD và tam giác BDC
có \(\widehat{DAB}=\widehat{CBD}\)
\(\widehat{ABD}=\widehat{BDC}\)(so le trong, AB // CD)
nên tam giác ABD đồng dạng với tam giác DBC
2
Xét tam giác ADC có
M là trung điểm của AD
N là trung điểm của AC
suy ra MN là đường trung bình của tam giác ADC
nên MN // DC (1)
Xét tam giác ABC có
K là trung điểm của BC
N là trung điểm của AC
suy ra NK là đường trung bình của tam giác ABC
nên NK //AB
mà AB // CD
do đó NK // CD (2)
Từ (1), (2) và theo tiên đề ơ-clít ta có
NK trùng với MN
do đó M,N,K thẳng hàng
Hình bạn tự vẽ nhé !
Câu 1:
Xét tam giác ABD và tam giác DBC có
Góc DAB = góc CBD
Góc ABD = góc BDC ( so le trong AB // CD )
nên tam giác ABD đồng dạng tam giác DBC
Câu 2:
Xét tam giác ADC có:
M là trung điểm của AD
N là trung điểm của AC
=> MN là đường trung bình của tam giác ADC => MN // DC (1)
Xét tam giác ABC có:
K là trung điểm của BC
N là trung điểm của AC
=> NK là đường trung bình của tam giác ABC => NK // AB
mà AB / CD => NK // CD (2)
Từ (1) và (2) theo tiên đề Ơ - clit ta có:
NK trùng với MN => M, N, K thẳng hàng ( đpcm )

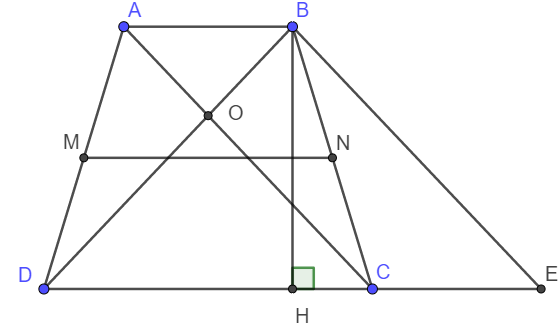
a) Xét tứ giác ABEC có AB // CE; AC // BE .
Vậy nên ABEC là hình bình hành. Suy ra AB = CE.
Do MN là đường trung bình hình thang ABCD nên ta có :
\(MN=\frac{AB+DC}{2}=\frac{CE+DC}{2}=\frac{DE}{2}.\)
b) Do ABCD là hình thang cân nên ta có:
\(AD=BC;DB=AC\)
Xét tam giác ABD và tam giác BAC có:
Cạnh AB chung
AD = BC
BD = AC
\(\Rightarrow\Delta ABD=\Delta BAC\left(c-c-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{BAC}\) hay \(\widehat{ABO}=\widehat{BAO}\)
Xét tam giác OAB có \(\widehat{ABO}=\widehat{BAO}\) nê OAB là tam giác cân tại O.
c) Do ABEC là hình bình hành nên AC = BE
Lại có AC = BD nên BD = BE
Suy ra tam giác BDE cân tại B.
Tam giác cân BDE có BH là đường cao nên đồng thời là đường trung tuyến.
Lại có theo câu a thì MN = DE/2
Giả thiết lại cho MN = BH. Vậy nên BH = DE/2
Xét tam giác BDE có trung tuyến BH bằng một nửa cạnh tướng ứng nên BDE là tam giác vuông tại B.
Vậy BDE là tam giác vuông cân tại B.

a) Hình thang cân ABCD, có:
AB // CD; AD = BC
Xét hình tam giác ACB, có:
I là trung điểm BC (gt)
Q là trung điểm AC (gt)
=> IQ là đường trung bình tam giác ACB
=> IQ // AB
mà AB // CD (cmt)
=> IQ // CD
Xét tam giác ACD, có:
Q là trung điểm AC 9gt)
P là trung điểm CD (gt)
=> QP là đường trung bình tam giác ACD
=> QP = 1/2 AD
mà AD = BC (I là trung điểm BC)
=> IB = IC = QP
Xét tứ giác QIPC, có:
QI // PC (cmt)
=> tứ giác QIPC là hình thang
có: QP = IC (cmt)
=> tứ giác QIPC là hình thang cân (đpcm)
b) Xét tam giác ABC, có:
QI là đường trung bình tam giác ABC (cmt)
=> tam giác CQI = 1/2 tam giác ABC
=> SQIC = 1/2 SABC
Cmtt: SCPQ = 1/2 SACD
mà mình thấy kì kì cái câu này theo mình là = 1/2 chứ sao = 1/4 (theo mình thôi nha)
c) Xét tam giác ABC, có:
M là trung điểm AB (gt)
Q là trung điểm AC (gt)
=> MQ là đường trung bình
=> MQ // BC
MQ = 1/2 BC
cmtt: MN // AD; MN = 1/2 AD
NP = 1/2; NP // BC
PQ // AD; QP = 1/2 AD
Xét tú giác MNPQ, có:
MQ // NP (cùng // BC)
MN // QP (cùng //AD)
=> MNPQ là hình bình hành
có: MQ = NP = 1/2 BC
=> MNPQ là hình thoi (đpcm)
p/s: có chỗ nào không hiểu thì inb hỏi nha ~

Nối BD. Gọi O là trung điểm DB
Xét tam giác ABD
Có: M là trung điểm AB ( gt)
O là trung điểm DB ( cách lấy O)
\(\Rightarrow\) OM là đường trung bình ABD
\(\Rightarrow\)OM // AD, OM = \(\frac{1}{2}\) AD ( đl)
\(\Rightarrow\)góc AEM = OMN ( 2 góc đồng vị) (1)
Tương tự ta chứng minh được ON là đường trung bình tam giác DBC
\(\Rightarrow\) ON // BC; BC
\(\Rightarrow\)góc OMN = MFB ( 2 góc so le trong) (2)
Mà AD = Bc (gt)
\(\Rightarrow\)OM=ON ( \(\frac{1}{2}\)AD)
Xét OMN
có OM = ON
\(\Rightarrow\) Tam giác OMN cân tại O ( đn)
\(\Rightarrow\) góc OMN = ONM ( đl) (3)
Từ (1); (2); (3) \Rightarrow góc AEM = MFB ( đpc/m)
Em dốt hình nên ko chắc đâu ạ! Mong mọi người check giúp em.
A B C D M N H I E
a) \(AC\cap MN=\left\{I\right\}\). Xét tam giác IAM:
Hiển nhiên ^IMA > ^IAM. Theo quan hệ giữa góc và cạnh đối diện suy ra IA > IM. (1)
Mặt khác, xét tam giác INC, hiển nhiên ^INC > ^ICN suy ra IC > IN(2)
Cộng theo vế (1) và (2) ta được AC > MN.
b)Trên tia đối HD lấy điểm E sao cho H là trung điểm DE. Khi đó
MH là đường trung bình tam giác DAE nên MH // AE. (3)
Mặt khác, dễ dàng chứng minh \(\Delta\)AHD = \(\Delta\)AHE
Suy ra ^ADH = ^AEH(*). Mà ABCD là hình thang cân nên ^ADC = ^BCD
Hay ^ADH = ^BCD (**). Từ (*) và (**) suy ra ^AEH = ^BCD
Mà chúng ở vị trí đồng vị nên AE // BC (4)
Từ (3) và ($) suy ra MH // BC (cùng song song với AE)
Suy ra đpcm.
"Từ (3) và ($).." -> "Từ (3) và (4)..." giúp em nha, em đánh nhầm