Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình như đề bài của bạn chưa hợp lí ^^
Mình sửa lại : \(AC^2+BD^2=AD^2+BC^2+2AB.CD\)
A B C D H K
Từ A và B lần lượt hạ các đường cao AH và BK (H,K thuộc CD)
Ta có : \(AC^2=AH^2+HC^2=AD^2-DH^2+\left(CD-DH\right)^2=AD^2+CD^2-2CD.DH\)
\(BD^2=BK^2+DK^2=BC^2-KC^2+\left(CD-CK\right)^2=BC^2+CD^2-2CK.CD\)
\(\Rightarrow AC^2+BD^2=AD^2+BC^2+2CD^2-2CD\left(DH+CK\right)=AD^2+BC^2+2CD^2-2CD\left(CD-AB\right)=AD^2+BC^2+2CD^2-2CD^2+2AB.CD=AD^2+BC^2+2AB.CD\)
cám ơn bạn nhiều nha, vì mình lấy cạnh AD là cạnh dưới còn BC là cạnh trên, điểm Gốc cạnh A nằm ở điểm D của bạn nên đề ra vậy chứ không sai , tks bạn nhiều nha

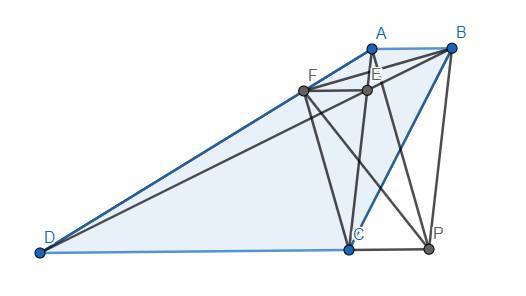
Dựng hình bình hành ABPC. Khi đó \(AD=AB+CD=CP+CD=DP\)
Ta có \(\dfrac{AB}{FE}=\dfrac{DA}{DF}\), \(\dfrac{CD}{FE}=\dfrac{DA}{AF}\)
\(\Rightarrow\dfrac{AB+CD}{FE}=DA\left(\dfrac{1}{DF}+\dfrac{1}{AF}\right)\)
\(\Rightarrow\dfrac{1}{FE}=\dfrac{DA}{DF.AF}\) \(\Rightarrow\dfrac{DF}{FE}=\dfrac{DP}{FA}\) \(\Rightarrow\dfrac{DF}{DC}=\dfrac{DP}{DA}=1\)
Từ đó \(\Delta DFC\) cân tại D. \(\Rightarrow\widehat{DFC}=\widehat{DCF}=\widehat{CFE}\) \(\Rightarrow\) FC là tia phân giác của \(\widehat{DFE}\). CMTT, FB là tia phân giác của \(\widehat{AFE}\). Do đó \(\widehat{BFC}=90^o\) (đpcm)

Xét tam giác \(ABD\)vuông tại \(A\):
\(BD^2=AB^2+AD^2\)(định lí Pythagore)
\(=4^2+10^2=116\)
\(\Rightarrow BD=\sqrt{116}=2\sqrt{29}\left(cm\right)\)
Lấy \(E\)thuộc \(CD\)sao cho \(AE\perp AC\)
Suy ra \(ABDE\)là hình bình hành.
\(AE=BD=2\sqrt{29}\left(cm\right),DE=AB=4\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AD\):
\(\frac{1}{AD^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AD^2}-\frac{1}{AE^2}=\frac{1}{100}-\frac{1}{116}=\frac{1}{715}\)
\(\Rightarrow AC=\sqrt{715}\left(cm\right)\)
\(AE^2=ED.EC\Leftrightarrow EC=\frac{AE^2}{ED}=\frac{116}{4}=29\left(cm\right)\)suy ra \(DC=25\left(cm\right)\)
Hạ \(BH\perp CD\).
\(BC^2=HC^2+BH^2=21^2+10^2=541\Rightarrow BC=\sqrt{541}\left(cm\right)\)
\(S_{ABCD}=\left(AB+CD\right)\div2\times AD=\frac{4+25}{2}\times10=145\left(cm^2\right)\)