Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

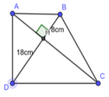
Xét ∆ ADB vuông tại A có: AH là đường cao ứng với cạnh huyền BD
⇒ A H 2 = HB. HD = 8.18 HA = 12 (cm) (hệ thức lượng trong tam giác vuông)
Xét ∆ ADC vuông tại D có: DH là đường cao ứng với cạnh huyền AC
⇒ H D 2 = H A . H C ⇒ 18 2 = 12 H C => HC = 27 (cm) (hệ thức lượng trong tam giác vuông)
Ta có: AC = AH + HC = 12 + 27 = 39 cm
BD = BH + HD = 8 + 18 = 26cm
S A B C D = A C . B D 2 = 26.39 2 = 507 c m 2
Đáp án cần chọn là: D

hệ thức lượng \(AB^2=AH\cdot AC\)
TÌM ĐƯỢC AC=15cm
suy ra HC=AC-AH=15-3=12cm

Bài 3:
a: \(=\left(cos^220^0+cos^270^0\right)+\left(cos^230^0+cos^260^0\right)+\left(cos^240^0+cos^250^0\right)\)
=1+1+1
=3
b: \(=5\left(1-sin^2a\right)+2sin^2a\)
\(=5-3sin^2a\)
\(=5-3\cdot\dfrac{4}{9}=5-\dfrac{4}{3}=\dfrac{11}{3}\)

Ta có: \(AH^2=HD.HB=18.8=144\Rightarrow AH=12\) (cm)
\(\Rightarrow AD=\sqrt{AH^2+HD^2}=\sqrt{12^2+18^2}=6\sqrt{13}\)
\(AB=\sqrt{12^2+8^2}=4\sqrt{13}\)
Ta có: \(DH^2=HA.HC\Rightarrow CH=\dfrac{DH^2}{HA}=\dfrac{18^2}{12}=27\)
\(\Rightarrow CD=\sqrt{CH^2+HD^2}=\sqrt{27^2+18^2}=9\sqrt{13}\)
\(\Rightarrow S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).AD=\dfrac{1}{2}\left(4\sqrt{13}+9\sqrt{13}\right).6\sqrt{13}\)
\(=507\left(cm^2\right)\)