Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

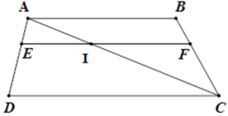
Gọi I là giao điểm của AC và EF.
Xét tam giác ACB có IF // AB nên theo định lý Ta-lét ta có
B F B C = A I A C = A E A D = 4 12 = 1 3 nên BF = 1 3 .BC = 1 3 .15 = 5 (cm)
Đáp án: B

a/
△ACD có:
- MN lần lượt đi qua trung điểm của AD và AC tại M và N
=> MN là đường trung bình của △ACD
Mặt khác, hình thang ABCD có:
- MP lần lượt đi qua trung điểm của AD và BC tại M và P
=> MP là đường trung bình của hình thang ABCD
=> MN trùng MP
Vậy: M, N, P thẳng hàng. (đpcm)
b/
- MN là đường trung bình của △ACD (cmt)
=> \(MN=\dfrac{1}{2}CD\)
Hay: \(MN=\dfrac{1}{2}.7=3,5\left(cm\right)\)
- MP là đường trung bình của hình thang ABCD (cmt)
=> \(MP=\dfrac{1}{2}AB.CD\)
Hay: \(MP=\dfrac{5+7}{2}=6\left(cm\right)\)
- \(NP=MP-MN\)
Hay: \(NP=6-3,5=2,5\left(cm\right)\)
- Nhận xét: Độ dài MP = 1/2 tổng độ dài hai đáy AB và CD
Vậy:
\(MN=3,5\left(cm\right)\)
\(NP=2,5\left(cm\right)\)
\(MP=6\left(cm\right)\)

E F A B C D o
gọi giao điểm của AC và EF là O
có EO//CD(EF//CD;O\(\in\)EF)
=>\(\frac{AE}{AD}=\frac{EO}{CD}\)(hệ quả ta-lét)
=>\(\frac{1}{3}=\frac{EO}{4}\left(CD=4cm;\frac{AE}{AD}=\frac{1}{3}\right)\)
=> EO=\(\frac{4}{3}\)cm
có BF=\(\frac{1}{3}\)BC(gt)=>CF=(1-\(\frac{1}{3}\))BC=\(\frac{2}{3}\)BC
Có FO//AB(EF//CD;O\(\in\)EF)
=>\(\frac{CF}{CB}=\frac{FO}{AB}\)(hệ quả talet)
=>\(\frac{2}{3}=\frac{FO}{1}\left(\frac{CF}{CB}=\frac{2}{3};AB=1cm\right)\)
=>FO=\(\frac{2}{3}\)cm
Có EO+FO=EF(O\(\in\)EF)
=>EF=\(\frac{4}{3}\)+\(\frac{2}{3}\)=\(\frac{6}{3}\)=2cm
vậy độ dài EF=2cm

Xét ΔADC có MI//DC
nên \(\dfrac{MI}{DC}=\dfrac{AM}{AD}=\dfrac{1}{2}\)
=>\(\dfrac{MI}{12}=\dfrac{1}{2}\)
=>\(MI=6\left(cm\right)\)
Xét hình thang ABCD có
M là trung điểm của AD
MN//AB//CD
Do đó: N là trung điểm của BC
Xét hình thang ABCD có
M,N lần lượt là trung điểm của AD,BC
=>MN là đường trung bình của hình thang ABCD
=>\(MN=\dfrac{AB+CD}{2}=\dfrac{6+12}{2}=\dfrac{18}{2}=9\left(cm\right)\)
\(\Delta\)MBC có AD // BC nên theo định lý Thales, ta có:
\(\frac{MA}{MB}=\frac{AD}{BC}\Rightarrow\frac{2,5}{BC}=\frac{5}{3}\)
\(\Rightarrow BC=\frac{2,5.3}{5}=\frac{3}{2}\)
Vậy \(BC=\frac{3}{2}cm\)
mk cứ thấy sai sai ý bn