Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

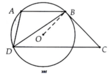
Chứng minh được: ∆DBC:∆BAD => D B C ^ = B A D ^
=> s đ D B C ⏜ = 1 2 s đ B m D ⏜
=> BC là tiếp tuyến của (O)

Đầu tiên ta chứng minh bổ đề sau:
A B C L T D M O
Cho tam giác \(ABC\) nội tiếp \(\left(O\right)\). Tiếp tuyến tại \(B,C\) của \(\left(O\right)\) cắt nhau tại \(T\). \(TA\) cắt lại \(\left(O\right)\) tại \(D\). \(M\) là trung điểm \(BC\). CM: \(\widehat{BAD}=\widehat{MAC}\).
Giải: Gọi \(L\) là trung điểm \(AD\). Khi đó \(\widehat{OBT}=\widehat{OCT}=\widehat{OLT}=90^o\) nên ngũ giác \(TBLOC\) nội tiếp.
Do vậy, \(\widehat{BLT}=\widehat{BCT}=\widehat{BDC}\). Suy ra cặp góc bù với chúng là \(\widehat{BLD}=\widehat{BAC}\).
Đến đây chứng minh được tam giác \(BLD,BAC\) đồng dạng.
Lập tỉ lệ cạnh rồi dựa vào trung điểm chứng minh được tam giác \(BAD,MAC\) đồng dạng.
Vậy 2 góc cần chứng minh bằng nhau (đpcm).
-------
Trở lại bài toán. (Ở phần dưới mình có dùng tính chất của phương tích và trục đẳng phương. Tuy ko có trong chương trình nhưng nó khá dễ và chứng minh được bằng kiến thức lớp 9. Bạn có thể tự tìm hiểu thêm).
Với lại hình của mình hơi sai một chút, mong bạn thông cảm.
L A B C D E F O K
Ý tưởng là ta sẽ chứng minh \(KO\) và hai tiếp tuyến tại \(C,D\) của đường tròn ngoại tiếp tam giác \(DOC\) đồng quy. Nếu làm được điều đó thì theo bổ đề trên sẽ có đpcm.
\(AB\) cắt đường tròn ngoại tiếp tam giác \(AOD,BOC\) lần lượt tại \(E,F\).
Khi đó \(\widehat{EDO}=\widehat{EAO}=\widehat{OCD}\) nên CM được \(ED\) tiếp xúc đường tròn ngoại tiếp tam giác \(DOC\).
CM tương tự thì \(FC\) cũng vậy.
Bây giờ cho \(ED\) cắt \(FC\) tại \(L\).
(Bạn thử tự CM \(LE=LF,LD=LC\) xem).
Do đó \(LE.LD=LF.LC\) nên điểm \(L\) có cùng phương tích đến 2 đường tròn 2 bên.
Vậy điểm \(L\) nằm trên trục đẳng phương của 2 đường tròn này, tức là đường thẳng \(OK\).
Ta đã CM được 3 đường cần CM đồng quy, theo bổ đề suy ra đpcm.