Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B D C E F
Theo đề ta có: \(AE+ED=AD\)
Và: \(\frac{AE}{DE}=\frac{3}{4}\Rightarrow\frac{AE}{AD}=\frac{3}{7}\)
Lại có: \(EF//AB//DC\)
Áp dụng định lí talet trong hình thang \(ABCD\) ta suy ra được:
\(\frac{BF}{BC}=\frac{AE}{AD}=\frac{3}{7}\)
Vậy .............

Giải:
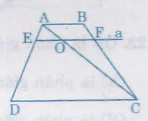
a) Nối AC cắt EF tại O
∆ADC có EO // DC => AEEDAEED = AOOCAOOC (1)
∆ABC có OF // AB => AOOCAOOC = BFFCBFFC (2)
Từ 1 và 2 => AEEDAEED = BFFCBFFC
b) Từ AEEDAEED = BFFCBFFC => AEED+AEAEED+AE= BFFC+BFBFFC+BF

Bạn tự vẽ lấy hình nha
gọi AC và EF cắt nhau tại I
Ta có : EO // DC ( Vì EF // DC )
Theo định lý Ta let:
\(\frac{ED}{AD}=\frac{OC}{AC}\)
\(\frac{BF}{BC}=\frac{AO}{AC}\)
\(\Rightarrow\)\(\frac{ED}{AD}+\frac{BF}{BC}=\frac{OC}{AC}+\frac{AO}{AC}=1\)
Vậy \(\frac{ED}{AD}=\frac{BF}{AC}=1\left(ĐPCM\right)\)

bn tham khảo ở đây
https://olm.vn/hoi-dap/tim-kiem?id=248114724967&id_subject=1&q=+++++++++++Cho+h%C3%ACnh+thang+ABCD+(+AB+//+CD),+m%E1%BB%99t+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+song+song+v%E1%BB%9Bi+%C4%91%C3%A1y+c%E1%BA%AFt+c%E1%BA%A1nh+b%C3%AAn+AD,+BC+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+%E1%BB%9F+E+v%C3%A0+F.Ch%E1%BB%A9ng+minh+r%E1%BA%B1ng:+EDAD+=FCBC+++++++++++
Câu hỏi của Mori Ran - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo

Em tham khảo nha.
Coi AB = 1, DC = k thì \(\frac{DO}{OB}=\frac{DC}{AB}=k\Rightarrow\frac{DO}{DB}=\frac{k}{k+1}\)
\(\Rightarrow OE=OF=\frac{k}{k+1}\Rightarrow EF=\frac{2k}{k+1}\)
Ta có \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{1}+\frac{1}{k}=\frac{k+1}{k}\)
\(\frac{2}{EF}=\frac{2}{\frac{2k}{k+1}}=\frac{k+1}{k}\)
Vậy nên \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{EF}\)