Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

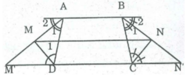
Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠ (M') = ∠ A 2 (sole trong)
∠ A 1 = ∠ A 2 (gt)
⇒ ∠ (M') = ∠ A 1 nên ∆ ADM' cân tại D
* DM là phân giác của ∠ (ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠ (N') = ∠ B 1 nên ∆ BCN' cân tại C.
* CN là phân giác của ∠ (BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ BN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN // M'N' (tính chất đường trung hình hình thang)
Hay MN//CD

a:
góc AMD=180 độ-góc MAD-góc MDA
\(=180^0-\dfrac{180^0-\widehat{BAD}}{2}-\dfrac{180^0-\widehat{ADC}}{2}\)
\(=180^0-\dfrac{1}{2}\widehat{ADC}-90^0+\dfrac{1}{2}\widehat{ADC}=90^0\)
Gọi giao của AM với DC là M'
Xét ΔDM'A có
DM là đường cao, là đường phân giác
nên ΔDM'A cân tại D
=>M là trung điểm của AM'
Gọi giao của BN với DC là N'
Ta có: \(\widehat{BNC}=180^0-\widehat{NBC}-\widehat{NCB}\)
\(=180^0-\dfrac{180^0-\widehat{ABC}}{2}-\dfrac{180^0-\widehat{BCD}}{2}\)
\(=180^0-90^0+\dfrac{1}{2}\widehat{ABC}-90^0+\dfrac{1}{2}\widehat{BCD}\)
=90 độ
Xét ΔCN'B có
CN vừa là đường cao, vừa là phân giác
nên ΔCN'B cân tại C
=>N là trug điểm của BN'
Xét hình thang ABN'M' có
M,N lần lượt là trung điểm của AM' và BN'
nen MN là đường trung bình
=>MN//CD//AB
b: MN=(AB+M'N')/2
=(AB+M'D+CD+CN')/2
mà M'D=AD và CN'=CB
nên MN=(AB+CD+AD+CB)/2

a. Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠(M') = ∠A2(sole trong)
∠A1= ∠A2(gt)
⇒ ∠(M') = ∠A1nên ΔADM' cân tại D
* DM là phân giác của ∠(ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠(N') = ∠B1nên ΔBCN' cân tại C.
* CN là phân giác của ∠(BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ PN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN = M'N' (tính chất đường trung hình hình thang)
Hay MN//CD
b)MN=AB+M′N′/2 (tính chất đường trung bình của hình thang)
⇒MN=AB+M′D+CD+CN′/2(1)
Mà M′D=AD,CN′=BC. Thay vào (1)
MN=AB+AD+CD+BC/2=a+d+c+b/2

xet tam giac ADM có
gocDAM=1/2 goc ngoai tai A
gocADM=1/2goc ngoai tai D
cong lai:gocADM+gocDAM=90*=> tam giac ADM vuông tại M
tương tự tam giac BNC vuông tại N
keo dai AM va` BN cắt CD tại E,F
xet tam giac ADE co DM vừa la` đường cao vừa la` phân giác => tam giac ADE can tai D=>DM la` trung tuyến =>M la` trung điểm AE
tương tự N la` trung diem BF
=> MN la` đuơng trung binh cua hinh thang AEFB =>MN//CD
