Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

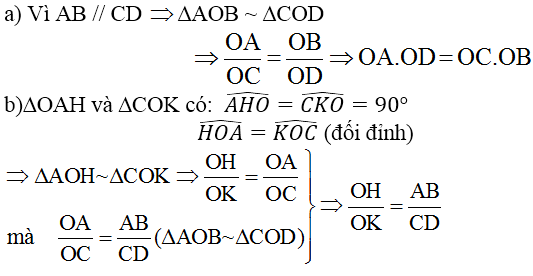
a;Vì AB//CD nên theo định lí Ta-lét ta có:
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
\(\Rightarrow OA.OD=OC.OB\)
b;Xét \(\Delta AOH\) và \(\Delta COK\)có:
\(\widehat{AHO}=\widehat{CKO=90^o}\)
\(\widehat{AOH}=\widehat{COK}\) (hai góc đối đỉnh)
\(\Rightarrow\Delta AOH~\Delta COK\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{OC}=\dfrac{OH}{OK}\left(1\right)\)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
\(\dfrac{AB}{CD}=\dfrac{OA}{OC}\left(2\right)\)
Từ 1 và 2 ta có:
\(\dfrac{OH}{OK}=\dfrac{AB}{CD}\)

a) AB//CD => góc BAC = góc DCA ( so le trong)
Xét tam giác ABO và tam giác CDO có:
góc BAC = góc DCA (cmt)
góc AOB = góc COD (đối đỉnh)
=> tam giác ABO ~ tam giác CDO (TH3)
=> \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\)
=> OA. OD = Oc. OB (đpcm)
b) Xét tam giác HOA và tam giác KOC có:
góc HOA = góc KOC (đối đỉnh)
góc BAC = góc DCA (cmt)
=> tam giác HOA ~ tam giác KOC (TH3)
c) Ta có:
+) AB//CD => \(\dfrac{AB}{CD}\) = \(\dfrac{OA}{OC}\)(hệ quả định lí Talet)(1)
+) AB//CD ; H \(\in\) AB; K \(\in\) DC => AH//KC
=> \(\dfrac{OH}{OK}\) = \(\dfrac{OA}{OC}\)( hệ quả định lí Talet)(2)
Từ (1) và (2) => \(\dfrac{AB}{CD}\) =\(\dfrac{OH}{OK}\) (đpcm)
![]()

Xét hình thang ABCD có EF//AB//CD
nên AE/AD=BF/BC(1)
Xét ΔADC có EO//DC
nên EO/DC=AE/AD(2)
Xét ΔBDC có OF//DC
nên OF/DC=BF/BC(3)
Từ (1), (2) và (3) suy ra OE=OF

a: Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
Do đó: ΔOAB đồng dạng với ΔOCD
Suy ra: OA/OC=OB/OD
hay \(OA\cdot OD=OB\cdot OC\)
b: Ta có: ΔOAB đồng dạng với ΔOCD
nên AB/CD=OA/OC=OB/OD
=>3/CD=2/4=OB/3,6
=>CD=6cm; OB=1,8(cm)

Câu 1

a, Vì tứ giác ABCD là hình thang
⇒ AB // CD
ΔCOD có AB // CD
⇒ ΔAOB ~ ΔCOD
⇒ \(\frac{OA}{OC}=\frac{OB}{OD}=\frac{AB}{CD}\)(đpcm)
b, Vì AB // CD ⇒ AM // CN
ΔCON có AM // CN
⇒ ΔAOM ~ ΔCON
⇒ \(\frac{OA}{OC}=\frac{OM}{ON}\)
mà \(\frac{OA}{OC}=\frac{AB}{CD}\)(câu a)
⇒ \(\frac{OM}{ON}=\frac{AB}{CD}\)
⇒ \(\frac{OM}{AB}=\frac{ON}{CD}\) (đpcm)
Câu 2
a, Vì ΔABC vuông tại A
⇒ \(\widehat{BAC}=90^0\)
Vì AH là đường cao của ΔABC
⇒ AH ⊥ BC
⇒ \(\widehat{H_1}=\widehat{H_2}=90^0\)
ΔABC và ΔHBA có
\(\left\{{}\begin{matrix}\widehat{BAC}=\widehat{H_1}=90^0\\\widehat{ABC}chung\end{matrix}\right.\)
⇒ ΔABC ~ ΔHBA (g.g)
⇒ \(\frac{AB}{HB}=\frac{BC}{AB}\) (1)
⇒ AB2 = BH . BC (đpcm)
b, ΔABC có BF là đường phân giác
⇒ \(\frac{BC}{AB}=\frac{FC}{FA}\) (2)
ΔABH có HE là đường phân giác
⇒ \(\frac{AB}{HB}=\frac{AE}{EH}\)(3)
Từ (1), (2), (3) ⇒ \(\frac{AE}{EH}=\frac{FC}{FA}\)
⇒ \(\frac{EH}{EA}=\frac{FA}{FC}\) (đpcm)
Chúc b ạn học tốt !!
ạn học tốt !!

a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó; ΔOAB\(\sim\)ΔOCD
Suy ra: OA/OC=OB/OD
hay \(OA\cdot OD=OB\cdot OC\)
b: Ta có; ΔOAB\(\sim\)ΔOCD
nên AB/CD=OB/OD=OA/OC
=>5/CD=OB/3,6=2/4=1/2
=>CD=10cm; OB=1,8(cm)