Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

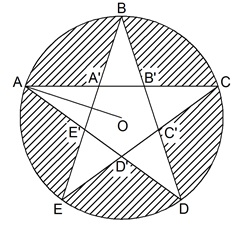
Đề không ghi rõ các giao điểm A',B',C',D',E' xác định như thế nào nên mình quy ước như sau:
AC cắt BE tại A'
AD cắt BE tại B'
AD cắt CE tại C'
BD cắt CE tại D'
BD cắt AC tại E'
Hình trong này hơi khó vẽ nên bạn tự vẽ hình đi nhé.
Bạn nên vẽ ngũ giác A'B'C'E'D' đều trước, rồi vẽ hình sao ABCDE sau (bằng cách kéo dài các cạnh để chúng cắt nhau)
Các bước giải bài toán:
+Chứng minh các tam giác A'B'A, B'C'E, C'D'D, D'E'C, E'A'B bằng nhau .
+Từ đó suy ra AC + AB' + AA' + A'B' = 2AC => Bài toán quy về tính AC
+Tính các góc trong ngũ giác -> trong tam giác -> góc OAC = 18 độ
+Tiếp theo bạn dùng tỉ lượng giác để tính cạnh AC khi đã biết OA=18 và góc OAC=18 độ.Bạn sẽ hạ OH vuông góc AC. Đây là kiến thức lớp 9. Do đó nếu cần bạn có thể kiểm tra và ghi rõ lại đề!
Đáp án: 60,8676
Chúc bạn học tốt.
Xin lỗi bạn mình nhầm một xí, đáp án đúng của bài toán phải là: 68,4761.
Mình bấm máy tính như sau: 2*2*18*cos(18)

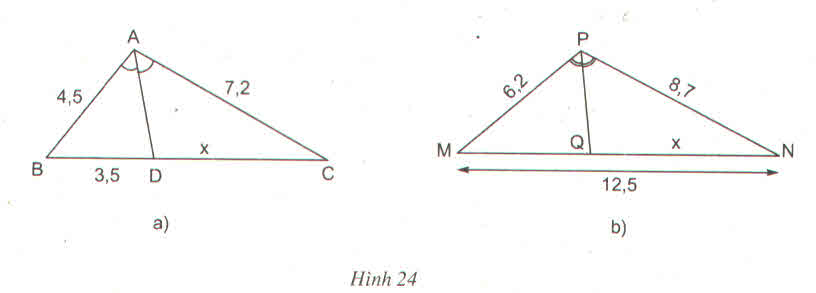
a)Vì AD là phân giác của góc BAC
=>\(\dfrac{DC}{BD}=\dfrac{AC}{AB}\) <=>\(\dfrac{x}{3.5}=\dfrac{7.2}{4.5}\) <=>x=\(\dfrac{7.2X3.5}{4.5}\) <=>x=5.6
b)vì PQ là phân giác của góc MPN
=>\(\dfrac{QN}{MQ}=\dfrac{PN}{PM}\) <=>
a) AD là tia phân giác của ∆ABC nên
BDABBDAB = DCACDCAC => DC = BD.ACABBD.ACAB = 3,5.7,24,53,5.7,24,5
=> x = 5,6
b) PQ là đường phân giác của ∆PMN nên MQMPMQMP = NQNPNQNP
Hay MP6,2MP6,2 = x8,7x8,7
Áp dụng tính chất của tỉ lệ thức:
=> x8,7x8,7 = MP6,2

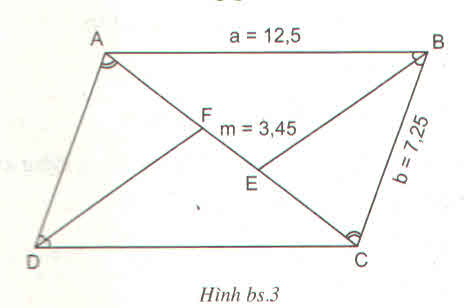
Ta có:
\(\widehat{ABC}=\widehat{ADC}\) và AD = BC = b = 7,25cm vì ABCD là hình bình hành.
Xét hai tam giác ADF và CBE ta có:
\(\widehat{ABC}=\widehat{ADC}\) (cmt)
AD = BC (cmt)
\(\widehat{DAF}=\widehat{BCE}\) (2 góc so le trong)
Vậy \(\Delta ADF=\Delta CBE\) (g-c-g).
=> AF = CE.
Cho AF = CE = x.
Áp dụng tính chất của đường phân giác BE trong tam giác ABC ta có:
\(\dfrac{AB}{BC}=\dfrac{AE}{CE}=\dfrac{AF+FE}{CE}\)
=> \(\dfrac{a}{b}=\dfrac{x+m}{x}=>x=\dfrac{mb}{a-b}\)= \(\dfrac{3,45.7,25}{12,5-7,25}=\dfrac{667}{140}\)
=> AC = \(2x+m=2.\dfrac{667}{140}+3,45=\dfrac{1817}{140}\approx12,98\)
Vậy AC \(\approx12,98\) cm.

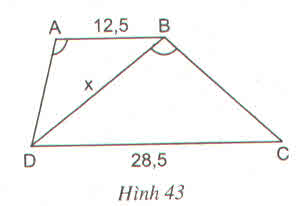
Xét ∆ABD và ∆BDC có:

=> ∆ABD ∽ ∆BDC(trường hợp 3)

=> BD = √(AB.DC) = √(12,5.8,5) = √356,25 => BD = 18,9 cm

Theo định lý Py-ta-go :
\(d^2=a^2+b^2=3^2+5^2=34\)
hay \(d=\sqrt{34}\approx5,8\left(cm\right)\)
Giả sử hình chữ nhật ABCD có AB = a = 3cm; BC = b = 5cm; BD = d
Trong tam giác vuông ABC theo định lý Py-ta-go ta có:
d2=a2+b2⇒d2=32+52=9+25=34d=√34≈5,8(cm)

a)
![]()
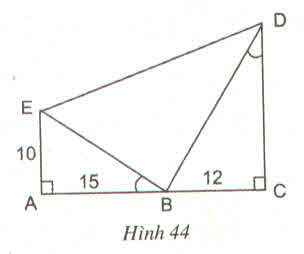
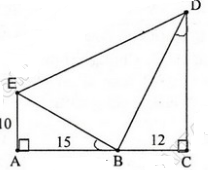
Vậy ∠EBD = 900
Vậy trong hình vẽ có ba tam giác vuông đó là:
∆ABE, ∆CBD, ∆EBD.
b) ∆ABE và ∆CDB có:
∠A = ∠C = 900
∠ABE = ∠CDB
=> ∆ABE ∽ ∆CDB => AB/CD = AE/CB
=> CD = AB.CB/AE
= 18 (cm)
∆ABE vuông tại A => BE =
![]() = 18 cm
= 18 cm
∆EBD vuông tại B => ED =
![]()
= 28,2 cm
c) Ta có: ![]()
= 1/2 . 10.15 + 1/2 . 12.18
= 75 + 108 = 183 cm2
SACDE = 1/2 (AE + CD).AC =1/2 (10+18).27=378 cm2
=> SEBD = SEBD – ( SABE + SDBC) = 378 – 183 = 195cm2




NHẦM QUỶ SATAN CHỨ
HAHA
QUỶ SANTA SẼ ÁM CẬU ĐÓ
NGÔI SAO LÀ KÍ HIỆU CỦA SANTA
HAHA