Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình khá khó nhìn nhé! Vào thống kê mình xem
Link: https://imgur.com/a/h2NM0ep

Đặt x là giao của AD và BE, Y là giao CF và AD; Z là giao BE và DF
Theo định lí Pascal thì M,X,Q; P,S,Y và R,Z,N là các bộ 3 điểm thẳng hàng
Xét tam giác XED có DF,CE, XQ đồng quy
Theo định lý Ceva có:
\(\frac{\sin\widehat{QXE}}{\sin\widehat{QXD}}\cdot\frac{\sin\widehat{ADF}}{\sin\widehat{EDF}}\cdot\frac{\sin\widehat{CED}}{\sin\widehat{CEB}}=1\)
\(\Rightarrow\frac{\sin\widehat{QXE}}{\sin\widehat{QXD}}=\frac{\sin\widehat{ADF}}{\sin\widehat{EDF}}\cdot\frac{\sin\widehat{CED}}{\sin\widehat{CEB}}=\frac{EF}{AF}\cdot\frac{CB}{CD}\)
Lập các tỉ số tương tự và nhân chúng lại với nhau, áp dụng định lý Ceva lần nữa cho tam giác XYZ ta có: XQ, YS, ZN đồng quy
hay MQ, PS, NR đồng quy (đpcm)
Goi AD giao BE tai X
Theo dinh ly Pascal ta se co MQ,PS,NR dong quy tai X
dpcm

Xét tam giác ABC, M là điểm trong tam giác, MD,ME,MF lần lượt là hình chiếu của M lên AB,AC,BC
Kẻ đường cao AH const
Đặt \(AB=AC=BC=a\)
\(S_{ABC}=S_{AMB}+S_{AMC}+S_{BMC}\)
\(=\frac{1}{2}\left(DM.AB+ME.AC+MF.BC\right)\)
\(=\frac{1}{2}a\left(DM+ME+MF\right)\)
\(=\frac{1}{2}a.AH\)
\(=DM+ME+MF=AH\left(đpcm\right)\)

Xét tam giác ABC, M là điểm trong tam giác, MD,ME,MF lần lượt là hình chiếu của M lên AB,AC,BC
Kẻ đường cao \(AH\) const
Đặt \(AB=AC=BC=a\)
\(S_{ABC}=S_{AMB}+S_{AMC}+S_{BMC}\\ =\dfrac{1}{2}\left(DM.AB+ME.AC+MF.BC\right)\\ =\dfrac{1}{2}a\left(DM+ME+MF\right)\\ =\dfrac{1}{2}a.AH\\ \Rightarrow DM+ME+MF=AH\\ \RightarrowĐpcm\)

a)
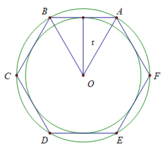
b) Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)
Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm
(Ta đã nêu được cách chia đường tròn thành sáu cung bằng nhau tại bài tập 10 SGK trang 71)
c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau ( định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây)