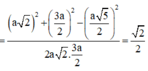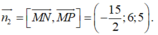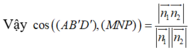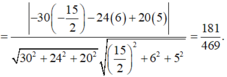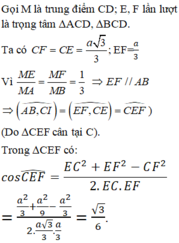Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

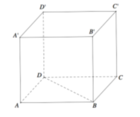
a: ABCD.A'B'C'D' là hình lập phương
=>AA'//BB'//CC'//DD' và AA'=BB'=CC'=DD'
Xét tứ giác AA'C'C có
AA'//CC'
AA'=CC'
Do đó: AA'C'C là hình bình hành
=>AC//A'C'
ABCD.A'B'C'D' là hình lập phương
=>ABCD và A'B'C'D' là hình vuông
ABCD là hình vuông
=>AC là phân giác của góc BAD và CA là phân giác của góc BCD
=>\(\widehat{BAC}=\widehat{DAC}=45^0\) và \(\widehat{BCA}=\widehat{DCA}=45^0\)
\(\widehat{A'C';BC}=\widehat{AC;BC}=\widehat{ACB}=45^0\)
b: Xét ΔBAC có M,N lần lượt là trung điểm của BC,BA
=>MN là đường trung bình của ΔBAC
=>MN//AC
Xét ΔA'AD' có
E,F lần lượt là trung điểm của AA',A'D'
=>EF là đường trung bình của ΔA'AD'
=>EF//AD'
ABCD.A'B'C'D là hình vuông
=>ADD'A' là hình vuông; DCC'D' là hình vuông
ABCD là hình vuông
=>\(AC=AB\cdot\sqrt{2}\)(1)
ADD'A' là hình vuông
=>\(AD'=AD\cdot\sqrt{2}=AB\cdot\sqrt{2}\)(2)
DCC'D' là hình vuông
=>\(CD'=CD\cdot\sqrt{2}=AB\cdot\sqrt{2}\left(3\right)\)
Từ (1),(2),(3) suy ra AC=AD'=D'C
=>ΔAD'C đều
=>\(\widehat{D'AC}=60^0\)
\(\widehat{MN;EF}=\widehat{AC;AD'}=\widehat{CAD'}=60^0\)
c: \(\widehat{MN;BC}=\widehat{AC;CB}=\widehat{ACB}=45^0\)
d: \(\widehat{EF;CC'}=\widehat{AD';DD'}=\widehat{AD'D}=45^0\)

Nhận xét:
Do tam giác A’B’D’ là tam giác đều nên C’M ⊥ A’D’
(C'A'D') ⊥ (AA'D'D) & (C'A'D') ∩(AA'D'D) ⇒ C’M ⊥ (AA’D’D)
Nên ∠(AC',(AA'D'D)) = ∠(C'AM) = 30 o .
Gọi K là trung điểm của DD’, ta có AKC’N là hình bình hành nên K với N đối xứng nhau qua trung điểm O của AC’. Mà O ∈ (AMC’), do đó
d[N,(C'MA)] = d[K,(C'MA)]
+ Xác định khoảng cách từ K đến (C’MA).
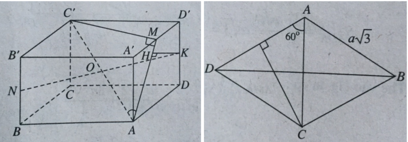
Do (C’MA) vuông góc với (AA’D’D) theo giao tuyến AM nên kẻ KH ⊥ AM, ta có KH ⊥ (C’MA) hay d[K,(C'MA)] = KH.
+ Tính KH.
Ta có: SAMK = SAA'D'D – (SAA'M + SMD'K + SADK) (1)
Trong tam giác AMC’, ta có: A M = C ’ M . c o t 30 o = ( 3 a √ 3 ) / 2 .
Trong tam giác AA’M, ta có: A A ’ = A M 2 - A ' M 2 = a √ 6 .


\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
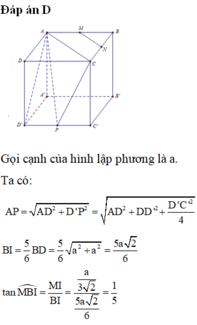
Ý A

Chọn A
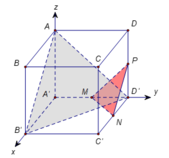
Đối với những bài cồng kềnh và tính toán rất phức tạp
thế này thì nên tọa độ hóa giải rất nhanh, khỏi phải mất nhiều
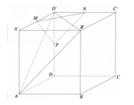
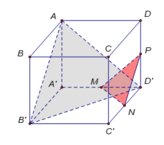
thời gian và tư duy. Gắn trục tọa độ Oxyz như hình vẽ bên với
A'(0;0;0), D(0;5;6), C' (4;5;0)
![]()
![]()
![]()
![]()
![]()