Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Bán kính đáy là R = a 2
Diện tích xung quanh hình trụ là S x q = 2 π R l = 2 π . a 2 .2 a = 4 π a 2 2

Đáp án C
Gọi cạnh của hình lập phương bằng a
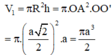
(R là bán kính đường tròn ngoại tiếp hình vuông ABCD)
Thể tích
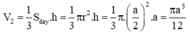
(r là bán kính đường tròn nội tiếp hình vuông ABCD)
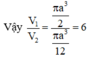

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

gọi x là cạnh của hình lập phương
Ta có
Stoàn phần= x2 X 4=144 (m2)
=> x=6 (m)
Thể tích của hình lập phương là:
V= x3=63 =216 (m3)

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2
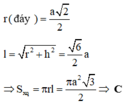



Đáp án C
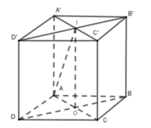
Do hình trụ và hình lập phương có cùng chiều cao nên ta chỉ cần chú ý đến mặt đáy như hình vẽ bên. Đường tròn đáy của hình trụ có bán kính bằng một nửa đường chéo của hình vuông ABCD; R = a 2 2
Do đó thể tích hình trụ cần tìm bằng S = 2 πRh = 2 π a 2 2 a = πa 2 2 .