Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Góc giữa AB và DD' = góc giữa AB và AA' ( vì DD'=AA')
Nên bằng 90 độ
\(\widehat{\left(AB,DD'\right)}=\widehat{\left(AB,AA'\right)}=\widehat{BAA'}=90^o\) do DD'//AA'.

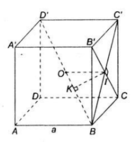
a) Ta có:
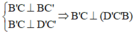
Gọi I là tâm hình vuông BCC'B'
Trong mặt phẳng (BC'D') vẽ IK ⊥ BD' tại K
Ta có IK là đường vuông góc chung của BD' và B'C
b) Gọi O là trung điểm của BD'
Tam giác BC’D’ có OI là đường trung bình nên :
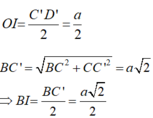
Vì ΔIOB vuông tại I có đường cao IK nên:
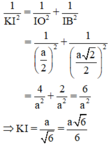

Đáp án D
Có hình chiếu của AC' xuống đáy là AC mà AC ⊥ BC nên AC'BD.

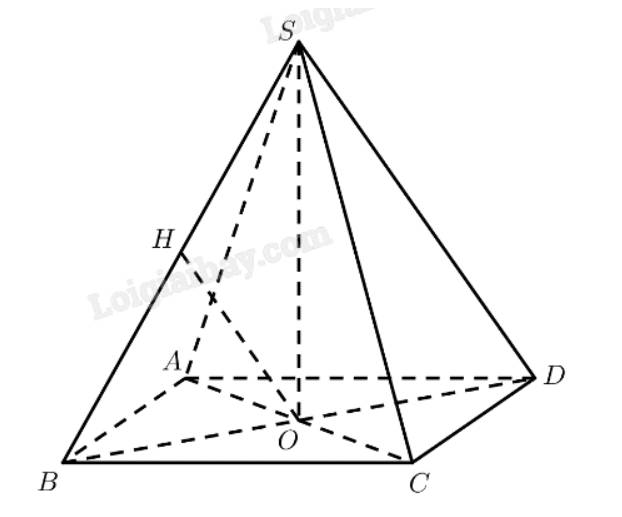
a) Kẻ \(OH \bot SB\left( {H \in SB} \right)\)
\(S.ABC{\rm{D}}\) là chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right) \Rightarrow AC \bot OH\)
Mà \(OH \bot SB\)
\( \Rightarrow d\left( {AC,SB} \right) = OH\)
\(B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông tại \(O \Rightarrow SO = \sqrt {S{B^2} - B{O^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông cân tại \(O\) có đường cao \(OH\)
\( \Rightarrow d\left( {AC,SB} \right) = OH = \frac{1}{2}SB = \frac{a}{2}\)
b) \({S_{ABC{\rm{D}}}} = A{B^2} = {a^2}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}\)


b) Ta có ACC' là tam giác vuông có cạnh \(AC=a\sqrt{2},CC'=a\)
Vậy \(AC'^2=AC^2+CC^2\Rightarrow AC'^2=2a^2+a^2=3a^2\)
Vậy \(AC'=a\sqrt{3}\)

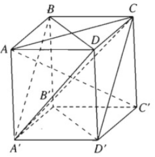
a) Ta có AB = AD = AA′ = a
và C ′ B = C ′ D = C ′ A ′ = a 2
Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’ . Vậy AC′ ⊥ (BDA′). Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà AC′ ⊥ (BDA′) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)
b) Ta có ACC’ là tam giác vuông có cạnh A C = a 2 và CC’ = a
Vậy A C ′ 2 = A C 2 + C C ′ 2
⇒ A C ′ 2 = 2 a 2 + a 2 = 3 a 2 . V ậ y A C ′ = a 3 .

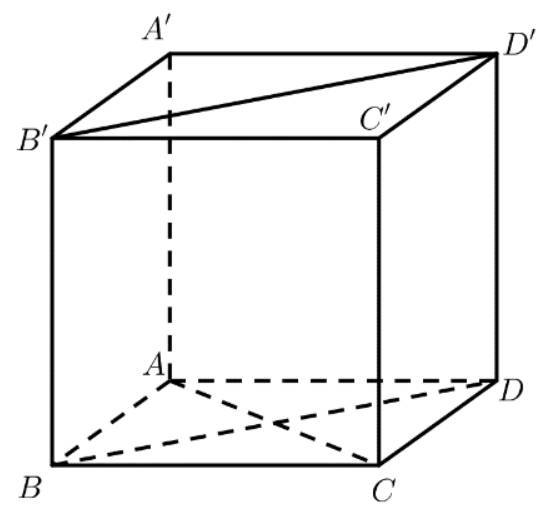
a) Các đường thẳng vuông góc với \(AC\) là: \(B{\rm{D}},B'D',AA',BB',CC',DD'\).
b) Các đường thẳng chéo với \(AC\) là: \(B'D',BB',DD'\).