Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
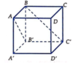
Đặt B ' 0 ; 0 ; 0 , A ' a ; 0 ; 0 , C ' 0 ; a ; 0 , B 0 ; 0 ; a ⇒ A a ; 0 ; a
Ta có B ' A → = a ; 0 ; a , B C ' → = 0 ; a ; − a , B ' B → = 0 ; 0 ; a
⇒ B ' A → , B C ' → = − a 2 ; a 2 ; a 2 ; B ' A → , B C ' → . B B ' → = a 3
d B ' A , B C ' = B ' A → , B C ' → . B B ' → B ' A → , B C ' → = a 3 3 a 4 = a 3 a 2 3 = a 3 3

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

Đáp án C.
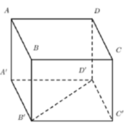
Giả sử các kích thước của hình hộp chữ nhật là A B = x , A D = y , A A ' = z . Trong đó x , y , z > 0 . Để giải bài toán, ta phân tích từng dữ kiện có trong đề bài.
1. Khoảng cách giữa hai đường thẳng AB và B'C bằng 2 a 5 5 .
Ta có
A B / / C D C D ⊂ A ' B ' C D A B ⊄ A ' B ' C D ⇒ A B / / A ' B ' C D ⇒ d A B ; B ' C = d A B ; A ' B ' C D
= d A ; A ' B ' C D = A H = 2 a 5 5 với H là hình chiếu của A trên .
Từ 1 A H 2 = 1 A A ' 2 + 1 A D 2 ⇒ 1 y 2 + 1 z 2 = 5 4 a 2 (1)
2. Khoảng cách giữa hai đường thẳng BC và AB' bằng 2 a 5 5 .
Tương tự, ta chứng minh được
B C / / A B ' C ' D ⇒ d B C ; A B ' = d B C ; A B ' C ' D
= B K = 2 a 5 5
với K là hình chiếu của B trên AB'.
Từ 1 B K 2 = 1 B A 2 + 1 B B ' 2 ⇒ 1 x 2 + 1 z 2 = 5 4 a 2 (2)
3. Khoảng cách giữa hai đường thẳng AC và BD' là a 3 3 .
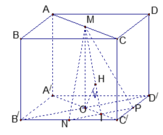
Gọi O = A C ∩ B D ⇒ O là trung điểm của BD. Gọi I là trung điểm của DD' thì OI là đường trung bình của Δ B D D ' ⇒ O I / / B D ' ⇒ B D ' / / A C I
⇒ d B D ' ; A C = d B D ' ; A C I = d D ' ; A C I = d D ; A C I
Ta thấy DI, DA, DC đôi một vuông góc với nhau nên:
1 d 2 D ; A C I = 1 D A 2 + 1 D C 2 + 1 D I 2 = 1 D A 2...

Đáp án D
Có hình chiếu của AC' xuống đáy là AC mà A C ⊥ B D nên A C ' ⊥ B D .




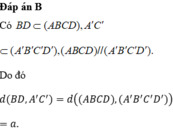
Đáp án D.
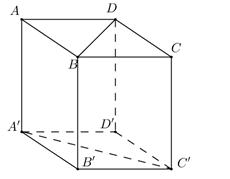
Cách 1: Gọi I là giao điểm của BC' và B'C . Trong B C ' D ' kẻ I H ⊥ B D ' tại H.
Ta có
B C ' ⊥ B ' C D ' C ' ⊥ B ' C B C ' , D ' C ' ∈ B C ' D ' ⇒ B ' C ⊥ B C ' D ' ⇒ B ' C ⊥ I H
Suy ra IH là đường vuông góc chung của BD' và B ' C ⇒ d B D ' , B ' C = I H .
Hai tam giác vuông BC'D' và BHI đồng dạng
⇒ I H D ' C ' = B I B D ' = a 2 2 a 3 = 6 6 ⇒ I H = a 6 6
Ta chọn D.
Cách 2: (Tọa độ hóa . Độc giả tự thực hiện)