Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
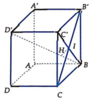
Cách 1: Gọi I là giao điểm của BC' và B'C . Trong B C ' D ' kẻ I H ⊥ B D ' tại H.
Ta có
B C ' ⊥ B ' C D ' C ' ⊥ B ' C B C ' , D ' C ' ∈ B C ' D ' ⇒ B ' C ⊥ B C ' D ' ⇒ B ' C ⊥ I H
Suy ra IH là đường vuông góc chung của BD' và B ' C ⇒ d B D ' , B ' C = I H .
Hai tam giác vuông BC'D' và BHI đồng dạng
⇒ I H D ' C ' = B I B D ' = a 2 2 a 3 = 6 6 ⇒ I H = a 6 6
Ta chọn D.
Cách 2: (Tọa độ hóa . Độc giả tự thực hiện)

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ B B ' D ' D
=> B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
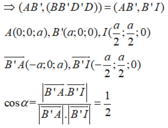

Đáp án A.
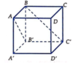
Đặt B ' 0 ; 0 ; 0 , A ' a ; 0 ; 0 , C ' 0 ; a ; 0 , B 0 ; 0 ; a ⇒ A a ; 0 ; a
Ta có B ' A → = a ; 0 ; a , B C ' → = 0 ; a ; − a , B ' B → = 0 ; 0 ; a
⇒ B ' A → , B C ' → = − a 2 ; a 2 ; a 2 ; B ' A → , B C ' → . B B ' → = a 3
d B ' A , B C ' = B ' A → , B C ' → . B B ' → B ' A → , B C ' → = a 3 3 a 4 = a 3 a 2 3 = a 3 3

làm đc chưa bạn...
gọiE là tđ AD
suy ra NA = NH = NMNM
gọi F là tđ AM thì c/m đc KN KM KA KD bằng nhau
vậy AMN cân vuông tại N

Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
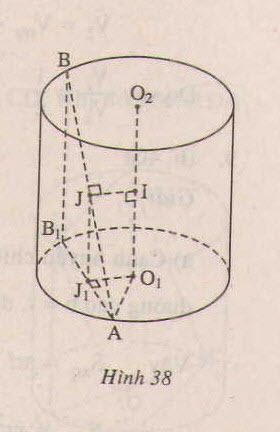
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :
Đáp án D
Có hình chiếu của AC' xuống đáy là AC mà A C ⊥ B D nên A C ' ⊥ B D .